Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.6 - Ex. 02
Desenhe o conjunto dado e calcule a área:
é o conjunto do plano limitado pelas retas , , e pelo gráfico de .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente desenhar o conjunto , que é definido como o conjunto do plano limitado pelas retas , , e pelo gráfico de . Isso quer dizer que temos uma função que está sendo limitada pelas retas constantes , , .
Então, basta a gente esboçar a função e as retas, para obtermos nossa região entre as curvas.
Além disso, vamos precisar calcular a área de e para isso vamos usar a integral de área entre curvas:
Vamos lá!
Passo 2
Vamos começar esboçando a nossa região:
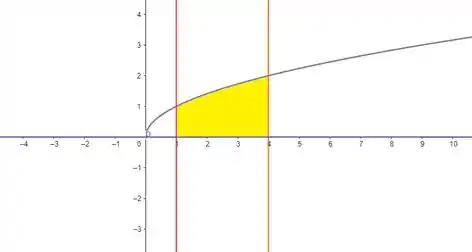
Temos a reta , em vermelho, a reta em laranja, a curva em cinza e o eixo em azul, que representa .
Repare que a região entre as curvas, pintada em amarelo, é a nossa região e é dessa região que nós vamos calcular a área agora.
Passo 3
Usando a fórmula da integral de área, vista no passo , vamos ter e (a função de cima menos a função de baixo). Além disso, repare que nossa região varia de até , de acordo com as retas verticais. Então, nosso intervalo de integração é .
Substituindo tudo, ficamos com:
E integrando, temos:
Aplicando os limites de integração:
Valeu, galera. Até a próxima! 😉