Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.6 - Ex. 03
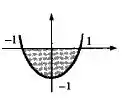
Desenhe o conjunto A dado e calcule a área:
A é o conjunto de todos (x, y) tais que .
Passo 1
Oi, pessoal! O problema pede para gente calcular uma área que está entre a função e .
Então vamos ter que desenhar essa área, achar os limites de integração e então resolver a integral definida.
Lembre-se: para desenhar a figura basta colocar os dados do problema, um de cada vez. O conjunto se encontra sempre entre as funções dadas e marcá-lo no desenho ajuda a visualizar e calcular.
Vamos lá!
Passo 2
Primeiro, vamos encontrar os pontos em que a função e se cruzam. A gente faz isso igualando,
Como, temos uma equação do segundo grau e o nosso é positivo, vamos ter uma parábola com concavidade para cima. Desenhando:
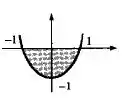
Pela figura vemos que a area vai de até , ou seja, esses são os limites de integração.
Vamos montar a integral!
Passo 3
A partir do desenho fica mais simples de montar a equação de área. O sinal negativo antes da integral se deve ao fato do conjunto estar abaixo do eixo y:
Agora é só resolver a integral,
Resposta
