Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 24

24. Encontre, com precisão de duas casas decimais, as coordenadas do ponto na curva y = s e n ( x ) que está mais próximo do ponto 4,2

Passo 1

Opa, bora pra mais uma questão?! O enunciado nos deu a seguinte função:

y = s e n ( x )

E pediu pra a gente encontrar, com precisão de duas casa decimais, as coordenadas do ponto que está mais próximo do ponto 4,2 .

Pra resolver esse problema vamos definir os pontos:

4,2

( x ,   s e n   x )

Usar a fórmula de distância pra calcular a distância entre esses dois pontos. Isso vai nos dar uma expressão, é ai que a gente calcula o mínimo usando derivada! Bora colocar a mão na massa?!

Passo 2

A distância entre dois pontos é dada pela seguinte fórmula:

Calculando sua distância até a origem:

d = x - x 0 2 + y - y 0 2

Substituindo:

d = x - 4 2 + ( s e n ( x ) - 2 2

Arrumando as coisas, temos:

d ( x ) = x 2 - 8 x + 16 + s e n 2 x - 4 s e n x + 4

Assim:

d ( x ) = x 2 - 8 x + s e n 2 x - 4 s e n x + 20

Para minimizar d ( x ) , basta minimizarmos o que está dentro da raiz:

a x = x 2 - 8 x + s e n 2 x - 4 s e n x + 20

Passo 3

Agora vamos derivar a ( x ) :

a ' x = 2 x - 8 + 2 s e n x cos ⁡ x - 4 cos ⁡ x

Igualando a zero para achar os pontos críticos:

a ' x = 0

Logo:

2 x - 8 + 2 s e n x cos ⁡ x - 4 cos ⁡ x = 0

Fazendo o gráfico de a ' ( x ) :

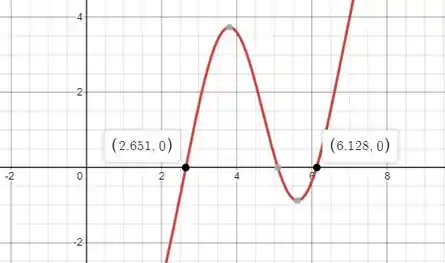
Passo 4

Agora vamos testar quais dos pontos estão mais perto de x = 4 . Usando a fórmula da distância:

d = x - 4 2 + ( s e n ( x ) - 2 2

x = 2,65 :

d ( 2,651 ) = ( 2,65 ) 2 - 8 ⋅ ( 2,65 ) + s e n 2 2,65 - 4 s e n 2,65 + 20

Logo:

d 2,65 = 2,04

x = 5,09 :

d ( 5,09 ) = ( 5,09 ) 2 - 8 ⋅ ( 5,09 ) + s e n 2 5,09 - 4 s e n 5,09 + 20

d ( 2,65 ) = 3,03

Portanto, o ponto mais próximo é o que possui x = 2,65 . Então,:

P = ( 2,65   ,   0,47 )

Prontinho!

Resposta

P = ( 2,65   ,   0,47 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A intensidade da iluminação em qualquer ponto de uma fonte de luz é proporcional ao quadrado da recíproca da distância entre o ponto e a fonte de luz.Duas luzes, uma tendo 8 vezes a intensidade da out
Uma folha de papel retangular 8,5 × 11p o l . É colocada sobre uma superfície plana. Um dos vértices é colocado no lado maior oposto, como mostra a figura, e deixado lá enquanto a folha está aplanada.
28. Suponha que um peso deva ser mantido 10m abaixo de uma reta horizontal A B por um fio com a forma de Y . Se os pontos A e B estão a uma distância de 8m um do outro, qual o fio de menor comprimento
42. Se dois corredores em ângulo reto um com o outro têm larguras de 3 e 4,5m, qual o comprimento da maior viga que pode ser movida horizontalmente, passando por essa quina? Despreze a dimensão transv
Nos Exercícios 29 e 30, use a expressão competição perfeita. Quando uma empresa funciona em competição perfeita, há muitas firmas pequenas assim, nenhuma empresa afeta o preço ao elevar a sua produção