Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 42
Calcule a integral:
Passo 1
Blzinha?
Legal galera, vamos integrar esta função:
Para resolver esse problema é importante lembrar algumas coisas:
A primeira, é que essa integral é tabelada, então temos:
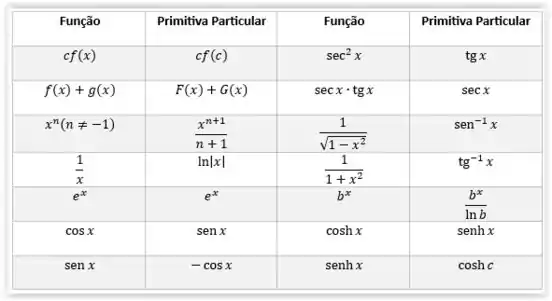
Essa função é a inversa do .
A segunda é que o é uma constante multiplicando a função, então podemos colocar ele pra fora e facilitar a nossa vida!
Terceira: vamos aplicar o TFC (teorema fundamental do cálculo), que nos diz:
Onde e , são as integrais da função, onde substituímos as variáveis pelos limites da integral. Onde e são constantes, ou seja, temos uma integral definida, também falamos que vamos avaliar a integral para os limites.
Agora sim, estamos prontos!
Passo 2
Agora bora resolver!
Colocamos o 4 para fora:
E agora aplicando a integral (da nossa tabela), repara que o continua multiplicando em? não esqueça dele:
Agora aplicamos o Teorema Fundamental do Cálculo aos limites de integração, aqui e :
Como a nossa integral é definida não usamos a constante de integração! Beleza?!
Prontinho!
