Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 25

25 . Uma estimativa anual dos usuários de telefone celular na Malásia, N (em milhares), é mostrada na tabela a seguir.

  1. Encontre a taxa média do crescimento.

( i ) de 1995 a 1997     ( i i ) de 1995 a 1996 ( i i i ) de 1994 a 1995.

Em cada caso, inclua as unidades.

( b ) Estime a taxa instantânea de crescimento em 1995 tomando a média de duas taxas médias de variação. Quais são as suas unidades?

( c ) Estime a taxa instantânea de crescimento em 199 5 medindo a inclinação da tangente.

Passo 1

Faremos as taxas sempre fazendo a divisão:

∆ N ∆ x

Em que ∆ P é a variação de usuários de telefone celular em milhares de pessoas e ∆ x é a variação do tempo em anos.

Passo 2

Fazendo a ( i ) taxa, que é de 1995 a 1997

∆ P ∆ x = N ( 1997 ) - N ( 1995 ) 1997 - 1995 = 2461 - 873 2 = 1588 2 = 794   m i l   u s u a r i o s / a n o

Fazendo a ( i i ) taxa, que é de 1995 a 1996

∆ P ∆ x = N ( 1996 ) - N ( 1995 ) 1996 - 1995 = 1513 - 873 1 = 640   m i l   u s u a r i o s / a n o

Fazendo a ( i i i ) taxa, que é de 1994 a 1995

∆ T ∆ x = N ( 1995 ) - N ( 1994 ) 1995 - 1994 = 873 - 572 1 = 301   m i l   u s u a r i o s / a n o

( b ) Faremos a média das duas últimas taxas, pois elas contém o ano de 1995 e tem uma distância de apenas 1   a n o   que calculamos na letra a .

T a x a   i n s t â n t a n e a = 640   + 301   2 = 941 2 = 470,5 m i l   u s u a r i o s / a n o

Passo 3

Deixaremos apenas o cálculo da tangente para o passo 3 , pois requer o desenho do gráfico e da tangente.

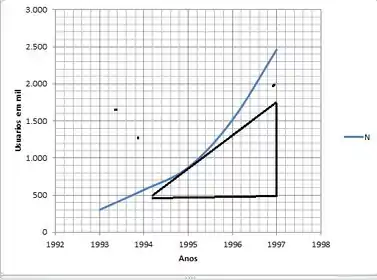
Pela tangente, iremos fazer algumas aproximações o cateto oposto vai de 500 até 1700 e o adjacente vai de 1994,2 a 1997 . Então, temos que:

t a x a   i n s t a n t â n e a = c a t   o p o c a t   a d j = 1700   -     500   1997 - 1994,2 = 1200 2 , 8 = 428,5 m i l h a r e s   d e   p e s s o a s / a n o

Devido as aproximações, chegamos a um valor bem perto da resposta!!

Resposta

a )

( i ) taxa

794   m i l   u s u a r i o s / a n o

( i i ) taxa 640   m i l   u s u a r i o s / a n o

( i i i ) taxa

301   m i l   u s u a r i o s / a n o

( b )

Taxa instantânea pela média é igual a :

470,5 m i l   u s u a r i o s / a n o

( c )

Taxa instantânea pela tangente é igual a :

428,5 m i l h a r e s   d e   p e s s o a s / a n o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra o gráfico da função f . Suponha que seja usado o método de Newton para aproximar a raiz r da equaçãofx = 0 com x 1 = 1 como aproximação inicial. (a) Desenhe as tangentes que são usadas
Para cada aproximação inicial, determine graficamente o que acontecerá se for usado o método de Newton para a função cujo gráfico é dado.(d) x 1 = 4
Encontre uma equação para a reta tangente à curva no ponto dado. Ilustre com o gráfico da curva e da reta tangente na mesma tela. y = 3 x 2 - x 3 ,( 1,2 )
Encontre uma equação para a reta tangente à curva no ponto dado. Ilustre com o gráfico da curva e da reta tangente na mesma tela. y = x - x ,( 1 , 0 )
Encontre as equações das retas tangentes à curva y = ln ⁡ x x Nos ponto 1,0ee , 1 e . Ilustre fazendo o gráfico da curva e de suas retas tangentes