Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.8 - Ex. 12
12. Seja . Estime o valor de de duas maneiras:
(a) Use a Definição 2 e tome os valores sucessivamente menores de .
(b) Dê um zoom sobre o gráfico de e estime a sua inclinação
Passo 1
Opa, e aí, tudo bem? Aqui temos:
E precisamos estimar:
Só que o enunciado pede pra a gente fazer de duas maneiras! Na primeira a gente vai usar a definição :
E pra segunda a gente vai plotar o gráfico de , dar um zoom bem perto de e vamos traçar uma reta tangente e calcular a sua inclinação fazendo:
Um desses pontos pode ser e o outro a gente vai estimar no olhometro! Bora lá?!
Passo 2
Vamos começar com a letra (a), temos:
Onde:
Agora a gente substitui na fórmula:
Agora a gente vai substituir pequenos valores de cada vez menores:
A ideia aqui é ir diminuindo os valores de :
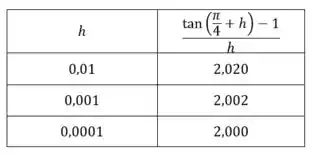
A medida que aproximamos de zero nos aproximamos de , então:
Passo 3
Agora, faremos a estimativa por meio do gráfico! Vamos plotar o gráfico:
E desenhar a reta tangente no ponto :
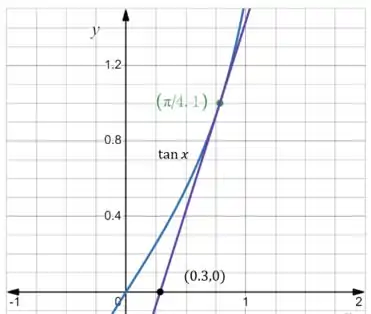
Aproximamos uma reta tangente, pegamos o ponto dado no enunciado e esse segundo ponto é um ponto qualquer pertencente a reta que a gente desenhou. Aqui foi no olhometro, beleza?!
Temos então a inclinação da reta:
Então por essa estimativa temos:
Bem próximo do que a gente encontrou lá em cima!
Resposta
(a)
(b)