Siga as instruções do Exercício 1(a), mas use como a aproximação inicial para encontrar a raiz .
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão fala pra gente seguir as instruções do exercício anterior para encontrar a raiz no gráfico dado por:
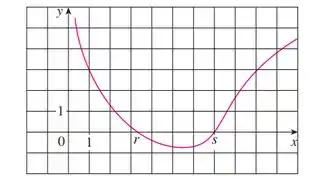
Teremos que supor que seja usado o método de Newton para aproximar a raiz da equação
Mas agora usando
como aproximação inicial.
O que teremos que fazer aqui desenhar as tangentes que são usadas para encontrar e , e estime os valores numéricos de e .
Para isso, precisamos lembrar que no método de Newton vamos considerar uma reta tangente à curva da função no ponto .
Depois devemos procurar a interseção de como o eixo , que será chamada de e verificar o quão próximo está da interseção da curva com o eixo .
Para encontrar , podemos fazer:
Depois, repetimos o processo, usando como uma segunda aproximação, fazendo:
E podemos repetir o processo quantas vezes for necessário. De modo geral, fazendo
E se ficar cada vez mais próxima da raiz de nossa curva à medida que cresce, fizemos que a sequência converge para .
Assim:
Perfeito.
Então, vamos nessa.
Passo 2
Podemos esboçar no gráfico as retas tangentes que precisamos.
Começando com , teremos:
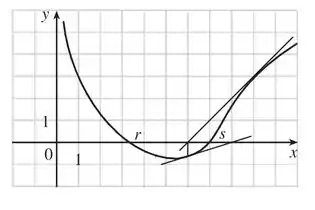
A linha tangente em intercepta o eixo em
Assim, faremos .
Agora a nossa nova linha tangente em intercepta o eixo em ,
então
Como não temos a função em mãos para usar a definição, fizemos a estimativa usando o prolongamento das retas.