Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.8 - Ex. 2
Para a função cujo gráfico é está ilustrado no Exercício 1, disponha os seguintes números em ordem crescente e explique seu raciocínio
Passo 1
E aí, pessoal!
Nesse problema foi dado um gráfico de uma função e nosso objetivo é colocar os valores de
Em ordem crescente.
Mas antes, vamos dar uma olhadinha no gráfico...
Parece complicado?
Para resolver esse problema vamos estimar os valores das imagens do gráfico em cada um dos pontos e em vamos esboçar a reta tangente a em e obter sua inclinação.
Isso porque nada mais é do que a inclinação da reta tangente a no ponto .
Agora parece fácil? Bora começar!
Passo 2
Vamos começar pelo mais simples... vamos estimar as imagens de nos pontos , e .
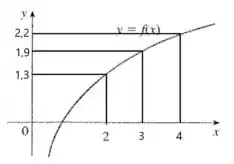
Fizemos essas estimativas a partir da escala do gráfico.
Agora vamos obter a inclinação da reta tangente a em .
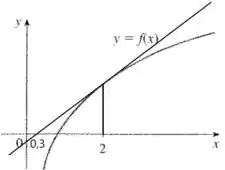
Agora precisamos de dois valores que pertence à reta para calcular sua inclinação...
Já temos o ponto que vimos anteriormente.
O outro ponto podemos obter a partir do ponto onde a reta corta o eixo ...
Estimando o valor em , temos
Portanto encontramos que
Tranquilo até aqui?
Passo 3
Agora só o que nos resta é organizar esses valores em ordem crescente...
Resumindo o que encontramos no passo 2, temos
Vamos começar calculando ...
Agora vamos calcular ...
Assim, temos que a ordem de é dada por
E aí! entendeu tudo? Responde Aí!