Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.18 - Ex. 25

25.Uma chapa tem a forma da região delimitada pelas curvas y = x 2 e y = 4 . Se esta chapa é imersa verticalmente na água, de tal forma que seu lado superior coincide com o nível d´água, determinar a força decorrente da pressão da água sobre um lado da chapa.

Passo 1

Para essas questão, usaremos a fórmula seguinte:

F = ∫ c d w k - y [ f y - g y ]

Em que g y é a função que limita a chapa a esquerda e f y é a função que limita a chapa à direita.

w é o peso por unidade de volume

k é o nível do líquido.

Passo 2

Vamos desenhar o “gráfico” da chapa, e assim conseguiremos tirar as informações que estão nessa integral.

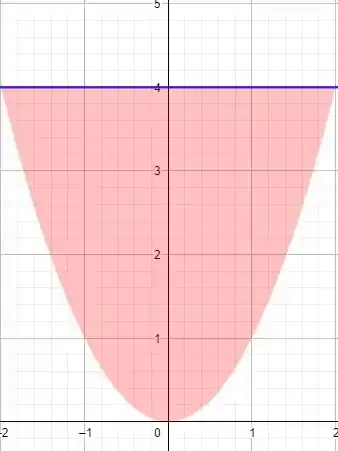
A comporta está em vermelho, é delimitada à esquerda pela função x = - y e à direita por x = y , pois y = x 2 .

Então, g y = - y e f y = y

Em azul é o nível da água, então k = 4   m , já que a comporta é limitada por y = 4 .

A comporta é delimitada superiormente por y = 4 e inferiormente por y = 0 . Então, d = 4 e c = 0 .

Passo 3

Substituindo tudo na integral e sabendo que o peso da água por metro cúbico é w = 9.807   N e w t o n .

F = ∫ c d w k - y f y - g y d y = ∫ 0 4 9807 ( 4 - y ) y - ( - y ) d y = 9807 × 2   ∫ 0 4 ( 4 - y ) y d y

Focando só na integral, temos:

F = 19.614 ∫ 0 4 4 y - y y d y = 19.614 ∫ 0 4 4 y 1 2 - y 3 2 d y = 19.614 8 3 y 3 - 2 y 5 5 4 0 = 19.614   64 3 - 64 5 = 19.614 × 128 1 5 = 167.372,8   N

Resposta

F = 167.372,8   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa quadrada com 1 m de lado é submersa verticalmente num tanque com água e seu centro está a 0,6 m abaixo da superfície. Ache a força decorrente da pressão do líquido sobre um lado da placa.
A face da comporta de uma barragem é vertical e tem a forma de um trapézio isósceles com 3 m no topo, 4 m na base e 3 m de altura. Se a base superior está a 20 m abaixo da superfície da água, ache a f
Uma placa com a forma de um triângulo retângulo isósceles é submersa verticalmente num tanque com água, com um cateto na superfície. Os catetos medem 6 cm cada.. Ache a força decorrente da pressão do
17. Ache o momento em torno da base mais baixa do trapézio da força do Exercício 15.
24. Resolva o Exercício 23 no caso em que a face do reservatório é um trapézio isósceles com 120 m de base maior no topo e 80 m de base menor e a distância entre as bases é de 40 m.