Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 26
26. Ache o volume do sólido gerado se a região do Exercício 24 girar em torno da reta .
Passo 1
Vamos entender como esse sólido está disposto e calcular o volume dele.
Passo 2
A região é a mesma do Exercício 24, só que vai girar em torno de . Olhando na figura:
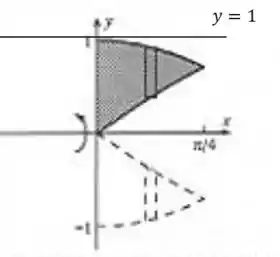
Passo 3
Como a única diferença é que a região vai girar em torno de outra reta, por simetria, podemos afirmar que o volume será igual ao encontrado no Exercício 24.
Por isso
Resposta
Exercícios de Livros Relacionados
7. y = x 2,y = x 3
6. y = ln x,y = - 1 ,y = 2ex = 0
9. y = 1 x,x = 0,y = 1 4ey = 4
4. y = cos x ,y = sen x,x = 0ex = π 4
12. y 2 = 2 x , x = 0 ,y = 0ey = 2 ,a or e d o rd oe i x od o sy .