Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.7 - Ex. 20
Determinar o volume do sólido gerado pela rotação, em torno da reta , da região limitada por
Passo 1
A região está mostrada na parte colorida da figura:
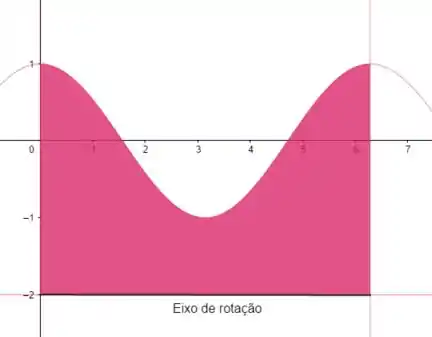
Passo 2
E aí o volume a gente calcula assim:
Vamos integrar agora:
Prontinho! Esse é o volume gerado pela rotação do sólido😉
Resposta
Exercícios de Livros Relacionados
9 - Determine o volume do sólido gerado pela rotação da região limitada à esquerda pela parábola x = y 2 + 1 e à direita pela reta x = 5 em torno:Do eixo xDo eixo yDa reta x = 5
9 - Determine o volume do sólido gerado pela rotação da região limitada à esquerda pela parábola x = y 2 + 1 e à direita pela reta x = 5 em torno:Do eixo xDo eixo yDa reta x = 5
Ache o comprimento do arco da curva y = ln sec x dex = 0 a x = π 4
Volume do hemisfério . Deduza a fórmula V = 2 3 π R 3 para o volume de um hemisfério de raio R comparando suas seções tranversáveis com as de um cilindro sólido circular reto de raio R e altura R , do
R limitada pelos gráficos de y = f x0 , x = a0 , x = ba e y = 0 . Se o volume do solido formado pela revolução de R em torno do eixo x for 4 π e o volume do sólido formado pela revolução de R em torno