Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.7 - Ex. 9

9. y = (1)/(x) , x = 0 , y = (1)/(4) e y = 4

Passo 1

Como estamos integrando em função de y, precisamos achar a f ( y ) que corresponde a f ( x ) dada:

f (x) = (1)/(x)

y = (1)/(x) = f ( y )

O gráfico dessa equação é o seguinte:

No eixo y temos: (1)/(4) <= y <= 4

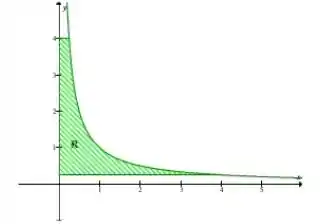
Passo 2

Para obtermos o volume gerado pela revolução de R em torno do eixo y, usaremos a seguinte formula:

V = pi int_a^b [f ( y )]^2 d y

Passo 3

Portanto, o volume é:

V = pi int_((1)/(4))^4 ((1)/(y))^2 d y

(pi (- (1)/(y))|_(1 // 4)^4 =

= pi (- (1)/(4) + (1)/((1)/(4)))

= pi (- (1)/(4) + 4) = (15 pi)/(4) u . v

Resposta

(15 pi)/(4) u . v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.Eixo y
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x Região, no primeiro quadrante, limitada acima pela reta y = 2 . Abaixo pela curva y =
36 - Use um teorema de Pappus para determinar o volume gerado pela rotação em torno da reta x=5 da região triangular delimitada pelos eixos coordenados e pela reta 2 x + y=6 .
Verifique as afirmações e fórmulas nos Exercícios 33 e 34.33 - As coordenadas do centroide de uma curva plana derivável são:
45 - Nos Exercícios 45 e 46, use um teorema de Pappus para determinar o centroide do triângulo dado. Use o fato de que o volume de um cone de raio r e altura h é V = 1 3 π r 2 h .