Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 28

26. Encontre a área do maior trapézio que pode ser inscrito num círculo com raio 1 e cuja base é o diâmetro do círculo

Passo 1

O enunciado nos pede pra encontramos a área do maior trapézio que pode ser inscrito num círculo com raio 1 e cuja base é o diâmetro do círculo. Lembrando que a área de um trapézio é dada por:

A = B + b h 2

Agora vamos desenhar um esquema do trapézio inscrito no círculo de r = 1 :

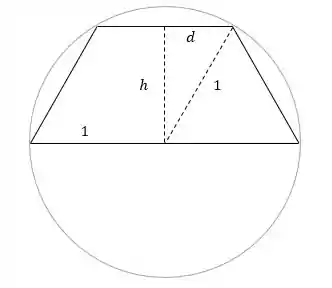
Podemos dizer que:

2 d = b

B = 2

E por Pitágoras:

1 2 = h 2 + d 2

Logo:

b 2 2 = 1 - h 2

b = 2 1 - h 2

Passo 2

Agora vamos partir para achar a área!

A = B + b h 2

Substituindo B   e b :

A = 2 + 2 1 - h 2 h 2

A = 1 + 1 - h 2 h

A área máxima pode ser calculada fazendo d A d h = 0 , para isso precisamos primeiro derivar nossa equação em função de h . Para isso vamos precisar usar a regra da cadeia e a regra do produto:

d A d h = 1 2 d h d h   1 + 1 - h 2 h + d 1 + 1 - h 2 h d h h

d A d h =   1 + 1 - h 2 + d 1 + 1 - h 2 d A h

d 1 + 1 - h 2 d h = - h h 2 - 1

d A d h =   1 + 1 - h 2 - h 2 1 - h 2

d A d h =   1 + 1 - h 2 - h 2 1 - h 2

d A d h = 1 - 2 h 2 1 - h 2 + 1

Passo 3

Igualando a 0 :

1 - 2 h 2 1 - h 2 + 1 = 0

Como a coisa não tá muito bonita, vamos fazer uma substituição de variável.

h 2 = u

Logo,

1 - 2 u 1 - u + 1 = 0

1 - 2 u = - 1 - u

Elevando ao quadrado:

1 - 4 u + 4 u 2 = 1 - u

Então:

4 u 2 = 3 u

u = 0 ou u = 3 / 4

Agora é só voltar para variável h e correr pro abraço:

h = 0 ou A = 3 / 2

Como h ≠ 0 :

h = 3 / 2

Então nossa área fica o seguinte:

A 3 2 = 1 2 ⋅ 2 + 2 1 - ( 3 / 2 ) 2 ⋅ 3 / 2  

Fazendo as contas:

A 3 2 = 3 3 4

Resposta

3 3 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

41. Uma viga de 27m é transportada horizontalmente por uma passagem com 8 m de largura, e então por um corredor em ângulo reto com a passagem. Qual deve ser a largura do corredor para que a viga possa
37. Ficou determinado que, excluindo-se os salários, o custo por quilômetro para operar um caminhão é de 8 + 1 300 x , onde x km/h é a velocidade do caminhão. Se os salários do motorista e do ajudante
33. Ache a menor distância da origem à reta 3 x + y = 6 , e encontre o ponto P sobre a reta que esteja mais próximo da origem. Então, mostre que a origem está na reta perpendicular à reta dada em P .
34. Ache a menor distância do ponto A 2 , 1 2 a um ponto sobre a parábola y = x 2 , e ache o ponto B sobre a parábola que seja o mais próximo de A . Então, mostre que A está sobre a reta normal da par
46. Prove, usando o método desta Secção, que a menor distância de um ponto P 1 x 1 , y 1 a uma reta l com equação A x + B y + C = 0 é A x 1 + B y 1 + C / A 2 + B 2 . (Sugestão: se s for o número de un