Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.3 - Ex. 27
27-28. Use um recurso gráfico para estimar o valor de fazendo um zoom no gráfico de ; depois compare sua estimativa ao valor exato obtido por derivação.
27.
Passo 1
Então pessoal, se plotarmos o gráfico da função em questão, teremos algo assim:
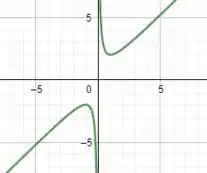
Se dermos um zoom em teremos o seguinte:
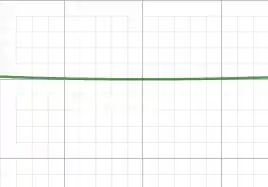
Ou seja, notamos que quanto mais aproximamos nosso gráfico do ponto em a tangente se aproxima de , pois se trata de uma reta horizontal. Dessa forma, graficamente chegamos à conclusão de que:
Agora vamos conferir algebricamente!
Passo 2
A função que nos foi dada é a seguinte:
Podemos simplifica-la da seguinte forma:
Utilizando a regra da potência, nossa derivada será:
Tudo bem, agora aplicando ponto , teremos:
Que é exatamente o resultado que esperávamos, galera! Às vezes analisar apenas o gráfico pode facilitar nossa vida, como pudemos ver!
Resposta
Graficamente parece que . Algebricamente temos: .