Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.1 - Ex. 45
Represente graficamente as curvas nos Exercícios 37-46
- Em que ponto os gráficos parecem ter tangentes verticais?
- Confirme as suas conclusões no item (a) com cálculos de limite. Mas, antes disso, leia a introdução dos Exercícios 35 e 36.
Passo 1
Para responder a letra a, vamos precisar fazer um esboço da função em um gráfico
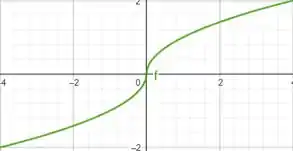
Olhando para o gráfico parece que a função possui tangente vertical em .
Passo 2
Precisamos definir com cálculos o que definimos na letra a. Para isso precisamos lembrar da definição de derivada
Passo 3
Em seguida vamos substituir o valor de definido
Quando , , logo
Passo 4
Aplicando os limites laterais
Como os limites laterais são iguais, f possui limite e como ele tende a , possui tangente vertical em .
Resposta
possui tangente vertical em
Exercícios de Livros Relacionados
(a) Encontre f n ( x ) , se f x = x n , n = 1 ,2 ,3 ...(b) Encontre f n ( x ) , se f x = x k , nk , onde k é um número inteiro positivo.(c) Encontre f n ( x ) se f x = a 0 + a 1 x + a 2 x 2 + … + a n
Encontre todos os pontos onde f não é diferenciável. Justifique sua resposta.(a) f x = 3 x - 2
Determine se a função dada é diferenciável em um valor x = x 0 , sendo que f está definida por fórmulas diferentes em lados diferentes de x 0 . Para isso, pode ser usado o resultado seguinte, que é um
Encontre as coordenadas de todos os pontos no gráfico de y = 1 - x 2 nos quais a reta tangente passa pelo ponto ( 2,0 ) .
Encontre condições em a , b , c e d para que o gráfico do polinômio f ( x ) = a x 3 + b x 2 + c x + d tenha:(a) exatamente duas tangentes horizontais; (b) exatamente uma tangente horizontal; (c) não t