Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.3 - Ex. 28
27-28. Use um recurso gráfico para estimar o valor de fazendo um zoom no gráfico de ; depois compare sua estimativa ao valor exato obtido por derivação.
28.
Passo 1
Então pessoal, se plotarmos o gráfico da função em questão, teremos algo assim:
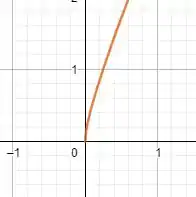
Se dermos um zoom em teremos o seguinte:
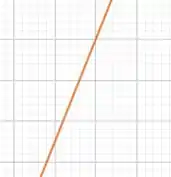
Mas poxa, o que conseguimos com isso? Simples, vamos descobrir a equação da reta nesse zoom! Se pegarmos dois pontos da reta, teremos o seguinte:
Primeiro ponto: ;
Segundo ponto: .
Lembrando que a equação da reta tangente é e que a derivada em é justamente nosso da equação, vamos dar continuidade à nossa busca!
Passo 2
Se criarmos um sistema, teremos:
Subtraindo as equações, teremos:
Opaaaa, descobrimos que nosso coeficiente angular vale , galera! Dessa forma, a nossa conclusão é que, graficamente, a derivada no ponto vale , ok? Agora vamos partir para os cálculos para comprovar isso ou não.
Passo 3
A função que nos foi dada é a seguinte:
Podemos simplifica-la da seguinte forma:
Utilizando a regra da potência, nossa derivada será:
Tudo bem, agora aplicando ponto , teremos:
Que é exatamente o resultado que esperávamos, galera!
Resposta
Graficamente parece que . Algebricamente temos: .