Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.4 - Ex. 27
27.(a) Se , encontre .
(b) Verifique que sua resposta para a parte (a) é razoável fazendo os gráficos de e para
Passo 1
Fala aí, tudo belezinha?
Bom, essa questão deu pra gene a função
E pediu para que respondêssemos a dois itens. No item a) precisaremos encontrar . Isto é, precisamos encontrar sua derivada. E para isso vamos analisar o tipo de função que temos para decidir qual a melhor regra de derivação que devemos usar.
Já no item b), precisaremos verificar que nossa resposta para a parte (a) é razoável fazendo os gráficos de e para . Aqui nós dependemos da função derivada que encontrarmos no item a), depois faremos seu gráfico pra ver se tudo faz sentido.
Mas, calma. Fica tranquilo que vou te mostrar tudinho no passo a passo.
Passo 2
(a)
Nossa função é:
E perceba que temos dois termos de tipos diferentes. Assim, para encontrar , teremos que usar a soma de derivadas. Ou seja, faremos:
Assim, temos que
Fazendo aquela anotação esperta de e :
Essa função é do tipo e sua derivada se dá pela regra . Assim:
Já para
essa aí é uma função trigonométrica e sua derivada é tabelada e dada por:
Substituindo na expressão da soma de derivada, ficamos com:
E prontinho, a primeira parte está feita, vamos para a analise do gráfico!
Passo 3
(b) agora vamos traçar o gráfico da função e de sua derivada . Veja:
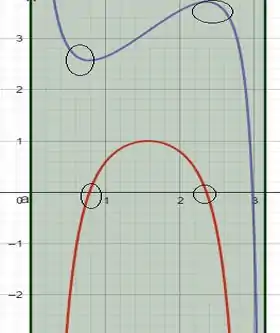
Tudo conforme imaginamos, quando a função tem valor máximo ou valor mínimo, é igual a zero. Que são as raizes da nossa derivada.
E em verde é o intervalo de a
Resposta
(a)
(b)
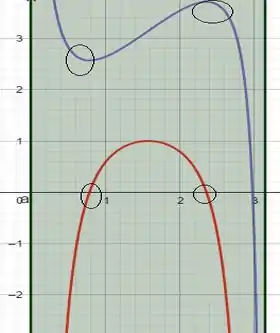
Quando a função tem valor máximo ou valor mínimo, é igual a zero.
E em verde é o intervalo de a