Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.2 - Ex. 29
Avalie a integral e interprete-a como a área de uma região. Esboce a região.
Passo 1
Pra inicio, vamos resolver a integral. Percebeu algo de interessante? Os intervalos são iguais, portanto, essa integral pode ser dividida em duas partes, logo pelo teorema da simetria:
Agora é só resolver normalmente!!
Fazendo...
Fazendo o nosso gráfico, temos:
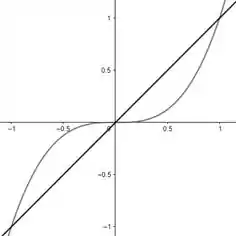
Prontinho!! Essa foi bem fácil
Resposta
Exercícios de Livros Relacionados
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais qued) 2 x 2 + y 2 ≤ 1ey ≥ 0
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais queg) x 2 ≤ y ≤ x .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais que 1 ≤ x ≤ 3e0 ≤ y ≤ x
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais queb) 1 2 ≤ x ≤ 2e0 ≤ y ≤ 1 x 2
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quee) y ≥ 0 ,1 ≤ x ≤ 2ex 2 - y 2 ≥ 1 .