Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.9 - Ex. 36
36. Uma tina horizontal tem 16 m de comprimento e seus extremos são trapézios isósceles com uma altura de 4 m, uma base menor de 4 m e uma base maior de 6 m . A água está fluindo entro da tina a uma taxa de . Com que velocidade o nível de água está subindo quando a profundidade da água é de 2 m ?
Passo 1
Opaaa, fala aí!! Vamos seguir os seguintes passos para resolver qualquer questão de taxas:
1- Leia cuidadosamente o problema.
2- Se possível, faça um diagrama.
3- Indentificar as variáveis e as constantes do problema.
4- Escreva uma equação que relacione as variáveis.
5- Derive em ambos os lados em relação a t usando regra da cadeia.
6- Substituir o que foi dado e encontrar o que foi pedido.
Passo 2
Se liga na ilustração do que a questão disse:
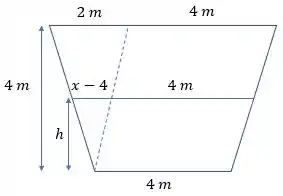
Essa é a tina vista de frente!
Nós precisamos saber quando . Como o problema diz que a água está fluindo a uma taxa de , repare nesse : isso é uma variação do volume!! Assim, vamos usar a fórmula do volume para relacionar as variáveis.
O volume dessa tina será a área da base vezes o comprimento:
O problema nos deu . Além disso, temos que a área da base é a área desse trapézio da figura:
No nosso caso, vamos usar o trapézio com bases e e altura (trapézio do meio da figura):
Substituindo no volume:
Opa, mas temos duas variáveis ainda e . Vamos relacioná-las!!
Passo 3
Vamos olhar para a figura de novo:
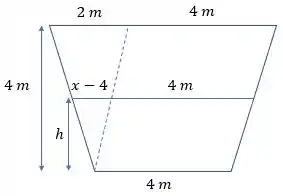
Hmmm, podemos relacionar e por semelhança de triângulos:
Passo 4
Beleza!! Agora, vamos voltar para a fórmula do volume, substituindo :
E vamos derivar os dois lados com relação ao tempo para achar :
Colocando em evidência:
Como queremos quando e, sabendo que :
Opaa, era isso que queríamos! Então, a altura está crescendo a uma taxa de quando .