Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 31
29-32 Determine se a afirmação falsa é verdadeira ou falsa. Explique a resposta.
31- Se a integral de no intervalo for negativa, então em cada
Passo 1
Essa questão é puramente conceitual, então vamos com calma para não nos embolarmos.
Para provarmos que uma afirmação matemática é falsa, precisamos apenas de um valor que foge a regra, então vai ser isso que buscaremos.
Passo 2
Mas por que vamos seguir por esse caminho?
Olha o teorema diz que se uma função é positiva (ou negativa) em um intervalo, então a sua integral é positiva (ou negativa), mas o que a questão nos diz é o contrário disso, então eu acho que é falsa essa afirmação!!
Você pode sempre tentar seguir por esse caminho, mas caso você não ache algo que foge a regra é melhor começar a se preparar para demonstrar que essa afirmação é verdadeira.
Passo 3
No passo 3, farei um gráfico de uma função que a integral é negativa num intervalo , porém essa função tem uma parte positiva, o que contradiz o enunciado!!
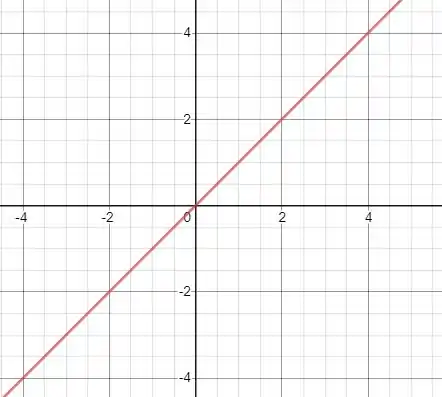
Essa função tem integral negativa de a , porém ela não é sempre negativa Ela tem uma parte positiva nesse intervalo
Resposta
Falsa