Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.6 - Ex. 5
Calcule o volume do sólido obtido pela rotação do círculo em torno
- do eixo
- da reta .
Passo 1
Para essa questão, vamos usar a fórmula proposta nas questões 3 e 4 desta mesma seção.
A equação dada se trata de um círculo da forma , onde são as coordenadas do centro e o raio. Olhando no plano temos:
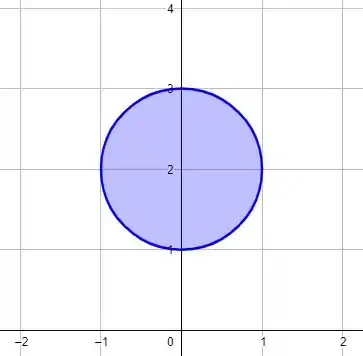
Passo 2
- Para o cálculo do volume, temos que pelo Teorema de Papus é dado por
- Já em torno da reta , temos a mesma fórmula
onde é o comprimento da circunferência gerada pela revolução do ponto que representa o centro de massa da figura e é a área da própria figura.
Como temos uma figura simétrica, podemos concluir nesse caso que o centro de massa coincide com o centro da circunferência que é , então o raio da circunferência de revolução, que é dado pela coordenada é e podemos calcular como
Já a área pode ser calculada pela área da circunferência
Então temos
Passo 3
Mas nesse caso o raio da circunferência de revolução é dado por , então temos
e é dado por
Como a área não muda temos