Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 33
33.Use o teorema para determinar se o valor da integral é positivo ou negativo
a)
b)
Passo 1
Vamos lá, a ideia dessa questão é que para sabermos o sinal da integral, precisamos olhar para o sinal da função nos intervalos de integração!!
Passo 2
Se você não entendeu muito bem, o que quero dizer é o seguinte! Se você quer saber o sinal da integral a baixo:
Você vai precisar saber o sinal da função abaixo:
No intervalo .
Então precisamos analisar o sinal de no intervalo e analisar o sinal de no intervalo .
Vamos por parte, começaremos com essa aqui
Essa função é positiva para qualquer valor maior que zero, então é positiva no intervalo .
Então só precisamos analisar a função no intervalo , vamos desenhar o gráfico dessa função nesse intervalo!
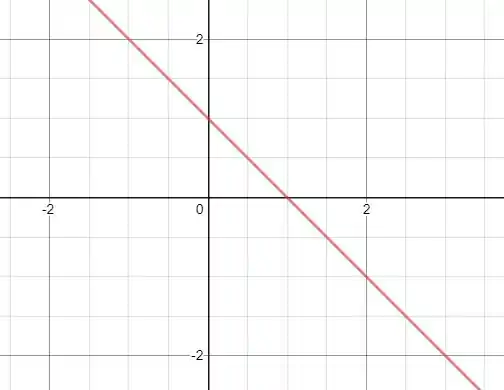
Essa função é negativa no intervalo de , então a função é negativa no intervalo , o que nos permite afirmar que a integral abaixo também é negativa.
Passo 3
Deixei para o passo 3, a questão da letra b). Vamos pensar da mesma forma.
Você vai precisar saber o sinal da função abaixo:
No intervalo .
Então precisamos analisar o sinal de no intervalo e analisar o sinal de no intervalo .
Vamos por parte, começaremos com essa aqui
Essa função é positiva para qualquer real então é positiva no intervalo .
Então só precisamos analisar a função no intervalo , vamos desenhar o gráfico dessa função nesse intervalo!
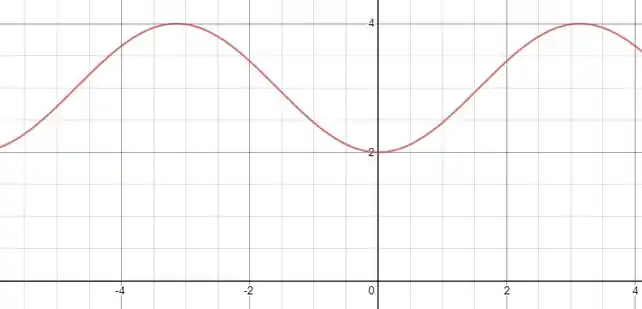
Essa função é positiva no intervalo de , então a função é positiva no intervalo , , o que nos permite afirmar que a integral abaixo também é positiva.
Resposta
- Negativa
- Positiva