Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.6 - Ex. 8
Calcule o volume do sólido obtido pela rotação do círculo em torno da reta .
Passo 1
Traçando a região dada e a reta no plano
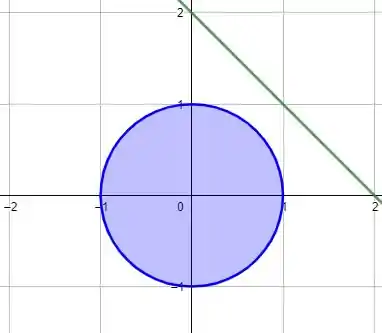
Utilizando o método da questão 4 temos que o volume vai ser dado por
onde é o comprimento da circunferência gerada pela revolução do ponto que representa o centro de massa da figura e a área da figura.
Para a área, podemos simplesmente usar a fórmula
Com
Passo 2
Para encontrar , precisamos da distância entre o centro de massa do círculo e a reta. O centro de massa do círculo coincide com o centro do próprio círculo, portanto é agora precisamos da distancia deste ponto para a reta.
A menor distância entre um ponto e uma reta vai ser o segmento que é perpendicular a reta, para isso vamos traçar outra reta perpendicular à e passa pela origem. Como essa reta tem inclinação , para ser perpendicular a nova reta precisa ter inclinação . A reta que tem inclinação e passa pela origem é a
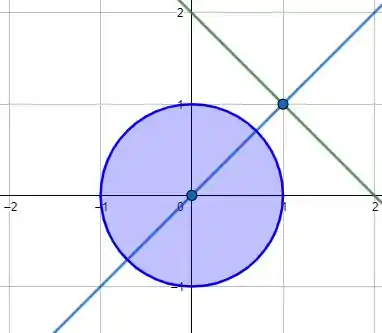
Agora precisamos encontrar em que ponto essa reta intersecta a reta , substituindo temos
No ponto , então precisamos da distância entre e
Passo 3
Com a distância entre o ponto e a reta, temos o raio da circunferência de revolução e podemos calcular o comprimento
Substituindo na fórmula do volume temos