Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 40

39-40 Calcule o limite expressando-o como integral definida no intervalo a , b e aplicando uma fórmula apropriada de geometria.

40 lim max ⁡ ∆ k → 0 ⁡ ∑ k = 1 n 4 - x k * 2 ∆ x k   ; a = - 2 , b = 2

Passo 1

Nós vamos usar a definição 5.5.1 para fazermos essa questão.

A definição é a seguinte:

lim max ⁡ ∆ k → 0 ⁡ ∑ k = 1 n f ( x k * ) ∆ x k = ∫ a b f x d x

Passo 2

Comparando a nossa definição com a da questão, temos que

lim max ⁡ ∆ k → 0 ⁡ ∑ k = 1 n 4 - x k * 2 ∆ x k = ∫ - 2 2 4 - x 2 d x

Então temos que calcular essa integral aqui:

∫ - 2 2 4 - x 2 d x

Passo 3

Paramos nessa expressão da integral

∫ - 2 2 4 - x 2 d x

Precisamos desenhar o gráfico de y = 4 - x 2 no intervalo de - 2 até 2 .

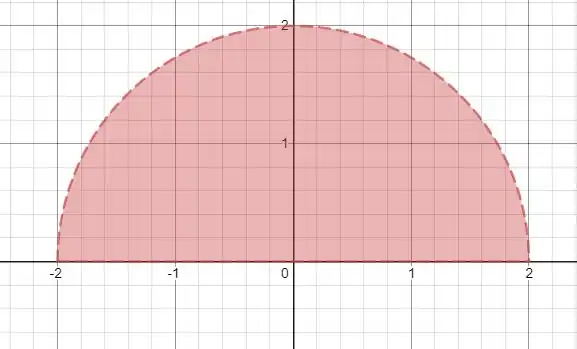
O gráfico dessa função é metade da circunferência , e a área da metade da circunferência é dada por:

A = π r 2 2

O raio, r , é igual a 2

A = π 2 2 2 = 4 π 2 = 2 π

A integral é numericamente igual a área, então:

∫ - 2 2 4 - x 2 d x = 2 π

Resposta

lim max ⁡ ∆ k → 0 ⁡ ∑ k = 1 n 4 - x k * 2 ∆ x k = ∫ - 2 2 4 - x 2 d x = 2 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∫ 0 1 x + x 4 d x
Calcule ∫ 1 2 x 3 + x + 1 x 3 d x
Calcule ∫ 0 1 1 1 + t 2 d t
Calcule ∫ - 1 1 e 2 x d x
Calcule ∫ 0 π 4 sin ⁡ x d x