Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.6 - Ex. 6

Calcule o volume do sólido obtido pela rotação da região x 2 + 4 y 2 ≤ 1 , em torno da reta y = 1 .

Passo 1

Utilizando o método da questão 4, o volume vai ser dado por

V = L ⋅ A

onde L é o comprimento da circunferência gerada pela revolução do ponto que representa o centro de massa da figura e A é a área da própria figura.

Para calcular A , vamos dividir a equação x 2 + 4 y 2 = 1 em duas funções, isolando o y

4 y 2 = 1 - x 2

Aplicando a raiz dos dois lados

2 y 2 = 1 - x 2

y = 1 - x 2 2

y = ± 1 - x 2 2

Podemos escrever também que y está entre duas funções, respeitando a inequação x 2 + 4 y 2 ≤ 1

- 1 - x 2 2 ≤ y ≤ 1 - x 2 2

Podemos então encontrar a variação de x igualando as duas funções

- 1 - x 2 2 = 1 - x 2 2

Somando 1 - x 2 2 em ambos os lados

1 - x 2 = 0

Elevando ao quadrado

1 - x 2 = 0

x 2 = 1

x = ± 1

E temos que nosso intervalo é dado por - 1 ≤ x ≤ 1 .

Passo 2

Calculando a área

A = ∫ - 1 1 1 - x 2 2 - - 1 - x 2 2 d x

= ∫ - 1 1 1 - x 2 2 + 1 - x 2 2 d x

= ∫ - 1 1 1 - x 2 d x

Vamos nos preocupar agora somente com a integral, depois voltamos com os limites de integração então temos

∫ 1 - x 2   d x

Utilizando a substituição trigonométrica

x = sen ⁡ θ d x = cos ⁡ θ   d θ

= ∫ 1 - sen 2 ⁡ θ ⋅ cos ⁡ θ   d θ

Utilizando a relação 1 - sen 2 ⁡ θ = cos 2 ⁡ θ ,

= ∫ cos 2 ⁡ θ d θ

Utilizando outra relação cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

= ∫ 1 + cos ⁡ 2 θ 2 d θ = θ 2 + sen ⁡ 2 θ 4 + C

Vamos agora retornar à variável x utilizando a função inversa do seno e o triângulo reto com sen ⁡ θ = x , ou seja, cateto oposto x e hipotenusa 1

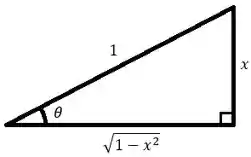
Temos que θ = arcsen ⁡ x e a relação sen ⁡ 2 θ = 2 sen ⁡ θ cos ⁡ θ , encontrando o seno e cosseno pelo triangulo temos

θ 2 + sen ⁡ 2 θ 4 + C = arcsen ⁡ x 2 + x ⋅ 1 - x 2 2 + C

Voltando agora aos limites de integração

∫ - 1 1 1 - x 2 d x = arcsen ⁡ x 2 + x ⋅ 1 - x 2 2 - 1 1

= arcsen ⁡ 1 2 + 1 ⋅ 1 - 1 2 2 - arcsen ⁡ ( - 1 ) 2 + - 1 ⋅ 1 - - 1 2 2

= π 4 - - π 4 = 2 π 4 = π 2

Passo 3

Para calcular L , precisamos somente da coordenada y do centro de massa, portanto vamos calcular

y c = 1 2 A ∫ a b g x + f ( x ) g x - f ( x )   d x

Substituindo a área e as funções temos

y c = 1 π ∫ - 1 1 1 - x 2 2 - 1 - x 2 2 1 - x 2 2 + 1 - x 2 2   d x

y c = 1 π ∫ - 1 1 0   d x = 0

Então temos que o raio da circunferência de revolução é r = 1 , que é distancia de y c até a reta y = 1 , logo

L = 2 π r = 2 π

E temos o volume

V = 2 π ⋅ π 2

V = π 2

Resposta

V = π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada parte, calcule a integral. Quando apropriado, use uma fórmula geométrica. ∫ - 1 1 ( 1 + 1 - x 2 ) d x ∫ 0 3 ( x x 2 + 1 - 9 - x 2 ) d x ∫ 0 1 x 1 - x 4 d x
Faça uma conjectura sobre as coordenadas do centroide da região e confirme-a por integração.
Conforme indica a figura ao lado, as massas m 1 = 5 , m 2 = 10 e m 3 = 20 estão posicionadas numa certa viga sem peso.Suponha que o fulcro esteja posicionado em x = 5 . Sem calcular a soma dos momento
Encontre o centroide da região.
Faça uma conjectura sobre as coordenadas do centroide da região e confirme-a por integração.