Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.11 - Ex. 21

int_0^4 | x^2 - 3 x + 2 | d x

Passo 1

Como estamos trabalhando com o módulo de x^2 - 3 x + 2 significa que toda a parte que seria negativa da função vai ser rebatida para cima do eixo x e ficar positiva.

Em questões desse tipo vamos sempre analisar a função em intervalos

A soma das raízes desse polinômio é 3 e o produto é 2, logo as raízes são 1 e 2, como ele tem concavidade para cima ele terá essa cara nosso gráfico

f (x) = |x^2 - 3 x + 2| = {- [[x^2 - 3 x + 2 , x <= 1],[x^2 + 3 x - 2 , 1 < x < 2],[x^2 - 3 x + 2 , x >= 2]])

Olha como fica a visualização da nossa integral

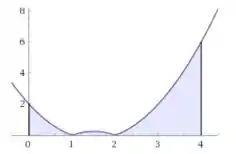
Passo 2

Lembra da nossa regra..

int_b^a (f (x) + g ( x )) d x = int_b^a f ( x ) d x + int_b^a g ( x ) d x

Vamos utilizá-la aqui

int_0^4 | x^2 - 3 x + 2 | =

= int_0^1 ( x^2 - 3 x + 2 ) d x + int_1^2 ( - x^2 + 3 x - 2 ) d x + int_2^4 ( x^2 - 3 x + 2 ) d x

= (x^3)/(3) - (3 x^2)/(2) + 2 x (​|_0 -> 1 - (x^3)/(3) + (3 x^2)/(2) - 2 x (​|_1 -> 2 + (x^3)/(3) - (3 x^2)/(2) + 2 x (​|_2 -> 4

(1)/(3) - (3)/(2) + 2 - (8)/(3) + (12)/(2) - 4 + (1)/(3) - (3)/(2) + 2 + (64)/(3) - (48)/(2) + 8 - (8)/(3) + (12)/(2) - 4 = (17)/(3)

Resposta

int_0^4 | x^2 - 3 x + 2 | d x = (17)/(3)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a derivada da função.59) y = int_(cos x)^(s e n x) ln ( 1 + 2 v ) . d v
Encontre a derivada da função.56) g x = ∫ 1 - 2 x 1 + 2 x t . s e nt . d t
Calcule a integral :int_0^2 | 2 x - 1 | d x
Calcule a integral : ∫ 0 3 2 ( d r 1 - r 2 )
Calcule a integral : ∫ π 4 π 3 csc 2 ⁡ θ d θ