Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 31c

31. Um modelo mais realista (do que o no Problema 30) para a trajetória de uma bola de beisebolinclui o efeito da resistência do ar. Nesse caso, as equações de movimento são

d v d t =   - r v

d w d t =   - g - r w

em que r é o coeficiente de resistência.

(a) Determine υ(t) e w(t) em termos da velocidade escalar inicial u e do ângulo inicial deelevação A.(b) Encontre x(t) e y(t) se x(0) = 0 e y(0) = h.(c) Desenhe as trajetórias da bola para r = 1/5, u = 125, h = 3 e para diversos valores de A.Como essas trajetórias diferem das do Problema 31 com r = 0?(d) Supondo r = 1/5 e h = 3, encontre a velocidade inicial mínima u e o ângulo ótimocorrespondente A para o qual a bola passa por cima de um muro que está a uma distância de350 pés e tem 10 pés de altura. Compare esse resultado com o do Problema 30(f)

Passo 1

No exercício anterior descobrimos que as equações de posição são

x = - 1 r e - r t + u t cos ⁡ A + 1 r

y =   - 1 r 2 e - r t - g t r + u t sen ⁡ A   + h + 1 r 2

Agora temos novos dados para podemos plotar gráficos de possíveis valores de A, ou seja, o ângulo de lançamento da bola.

x = - 5 e - t / 5 + 38 t cos ⁡ A + 5

y =   - 25 e - t 5 - 50 t + 38 t sen ⁡ A   + 0.9 + 25

Passo 2

Vamos plotar os gráficos agora

A = 30 °

A = 45 °

A = 60 °

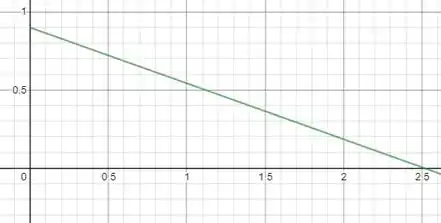
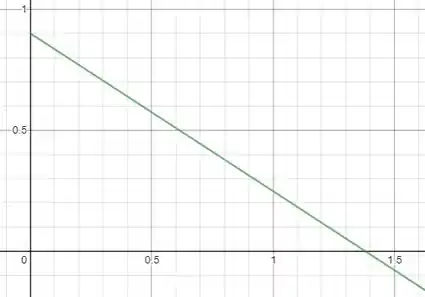
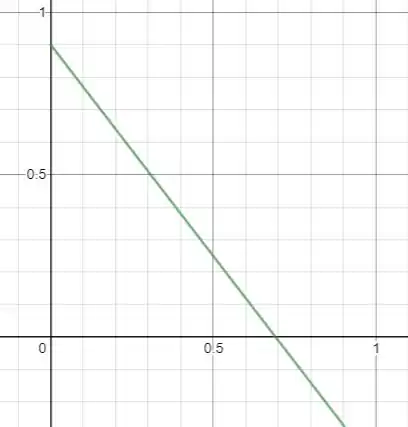
Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

19. Considere um lago, de volume constante V, contendo, no instante t, uma quantidade Q(t) de poluentes distribuídos uniformemente em todo o lago com uma concentração c(t), onde c(t) = Q(t)/V. Suponha
19. Considere um lago, de volume constante V, contendo, no instante t, uma quantidade Q(t) de poluentes distribuídos uniformemente em todo o lago com uma concentração c(t), onde c(t) = Q(t)/V. Suponha
23. Um paraquedista pesando 180 lb (incluindo o equipamento) cai verticalmente de uma altura de5000 pés** e abre o paraquedas depois de 10 s de queda livre. Suponha que a força deresistência do ar, qu
25. Um corpo de massa m é projetado verticalmente para cima com uma velocidade inicial υ0 emum meio que oferece uma resistência k|υ|, em que k é constante. Não leve em consideraçãovariações na força g
24. Um trenó foguete, com velocidade inicial de 150 milhas/h (≈ 240 km/h), é freado por um canalde água. Suponha que, enquanto está sendo freado, a aceleração a do trenó é dada por a(υ) = –μυ², em que