32. O Problema da Braquistócrona. Um dos problemas famosos na história da matemática é oproblema da braquistócrona:9 encontrar uma curva ao longo da qual uma partícula desliza sematrito em um tempo mínimo de um ponto dado P até outro ponto Q, em que o segundo ponto estámais baixo do que o primeiro, mas não diretamente debaixo (veja a Figura 2.3.6). Esseproblema foi proposto por Johann Bernoulli em 1696 como um desafio para os matemáticos daépoca. Johann Bernoulli e seu irmão Jakob Bernoulli, Isaac Newton, Gottfried Leibniz e omarquês de L’Hôpital encontraram soluções corretas. O problema da braquistócrona éimportante no desenvolvimento da matemática como um dos precursores do cálculo dasvariações.Ao resolver esse problema, é conveniente colocar a origem no ponto superior P e orientar os eixos conforme ilustrado na Figura 2.3.6. O ponto mais baixo Q tem coordenadas (x0, y0).possível mostrar, então, que a curva de tempo mínimo é dada por uma função y = ϕ(t) qsatisfaz a equação diferencial
em que k2 é certa constante positiva a ser determinada mais tarde.(a) Resolva a Eq. (i) para y′. Por que é necessário escolher a raiz quadrada positiva?(b) Introduza uma nova variável t pela relação
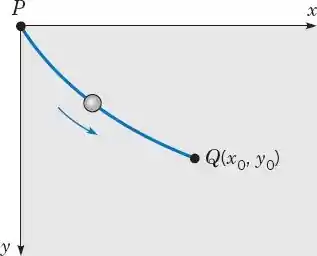
FIGURA 2.3.6 A braquistócrona.
Mostre que a equação encontrada no item (a) fica, então, na forma
(c) Fazendo θ = 2t, mostre que a solução da Eq. (iii) para a qual x = 0 quando y = 0 é dada porAs Eqs. (iv) são equações paramétricas da solução da Eq. (i) que contém o ponto (0, 0). Ográfico das Eqs. (iv) é chamado de cicloide.(d) Se fizermos uma escolha apropriada da constante k, então a cicloide também contém oponto (x0, y0) e é a solução do problema da braquistócrona. Encontre k, se x0 = 1 e y0 = 2
Passo 1
Conseguimos achar no item b) a seguinte relação
Agora o enunciado nos pede para integrar essa função e achar
O enunciado quer que façamos a seguinte substituição , com isso nossa função fica
Passo 2
Agora só precisamos encontrar uma relação para
Existe uma identidade trigonométrica que nos diz
Vamos usa-la agora e substituir na nossa função
Lembrando que o enunciado pede para fazermos
Conseguimos provar o que o exercício nos pede. Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)