Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.8 - Ex. 32
A expectativa de vida melhorou significativamente no século . A tabela fornece os valores de , a expectativa de vida no nascimento (em anos) de um menino no ano nos Estados Unidos. Interprete e estime os valores de e .
Passo 1
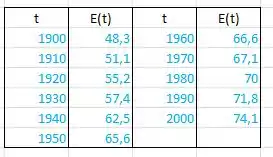
Opa, bora lá! O enunciado nos dá uma tabela da expectativa de vida ao longo dos anos:
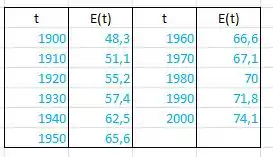
Sabendo disso a gente precisa estimar e e interpretar os resultados! Devemos lembrar que a derivada pode ser interpretada como uma taxa de variação e essa definição que usaremos nesses problemas.
Nesta situação, a derivada é a taxa de crescimento da expectativa de vida em um dado momento. Em outras palavras, quanto tende a aumentar do ano em direção ao seguinte.
E pra calcular esses valores, vamos usar a definição de derivada:
Passando pras nossas variáveis:
Vamos ver isso na prática!
Passo 2
Considerando o que discutimos no passo 1, podemos dizer que:
- é taxa de variação da expectativa de vida no ano de
- é taxa de variação da expectativa de vida no ano de
Passo 3
Da definição que vimos no passo 1 pra derivada:
Vamos calcular nosso primeiro valor
Agora pensa comigo quem vai ser . A rigor, ele não tem um valor definido, mas percebe que ele tende a zero, então faz sentido a gente pegar a menor variação possível certo?
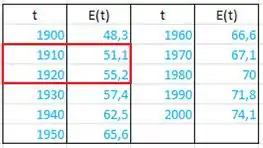
Vamos considerar o ano seguinte de que temos dados:
Então a derivada fica:
Passo 4
Agora vamos fazer a mesma coisa pra
Vamos também usar o dado imediatamente seguinte
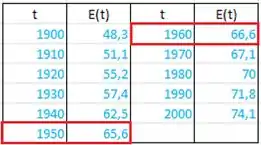
Então
Não esqueça das unidades hein! Taxa tem um significado teórico, no nosso caso é a variação dos
Logo
Prontinhoo!
Resposta
é taxa de variação da expectativa de vida no ano de e é taxa de variação da expectativa de vida no ano de .