Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.3 - Ex. 33

33-34 Use o gráfico para estimar a abscissa dos pontos de inteerseção das curvas dadas. Então use essa informação e sua calculadora para estimar o volume do solido obtido pela rotação sobre o eixo y da regição fechada sobre essas curvas.

33. y = x 2 - 2 x , y = x x 2 + 1

Passo 1

Antes de botarmos qualquer grafite no papel, vamos para o computador e fazer o gráfico dessas funções. Eu utilizo o geogebra, porém você quem sabe qual vai utilizar!

Passo 2

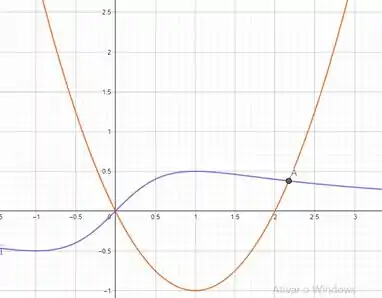
Em laranja, é a nossa parábola

y = x 2 - 2 x .

Em roxo, é a função

y = x x 2 + 1

E o ponto de encontro é aquele ponto A, vou colocar com três casa decimais, acredito que seja um bom valor. O ponto A tem abscissa igual a: 2,174 .

Passo 3

Então, o volume da região fechada em torno de y é dada por:

V = 2 π ∫ 0 2,174 x x x 2 + 1 - ( x 2 - 2 x ) d x

Vamos resolver essa integral:

V = 2 π ∫ 0 2,174 x x x 2 + 1 - ( x 2 - 2 x ) d x = 2 π ∫ 0 2,174 x 2 x 2 + 1 d x - ∫ 0 2,174 ( x 3 - 2 x 2 ) d x

Resolveremos uma de cada vez, vamos para a mais fácil que é

∫ 0 2,174 ( x 3 - 2 x 2 ) d x = x 4 4 2,174 0 - 2 3 x 3 2,174 0 = - 1,264

Sabe aquela integral que você nunca grava? Mas ela está nas integrais imediatas, então nessa integral teremos que utilizá-la.

∫ d x x 2 + 1 = tan - 1 ⁡ x

A integral acima é daquelas que a gente nunca grava, mas é imediata!!!

Agora vamos fazer a integral da questão, porém sem os valores nos limites!

∫ x 2 x 2 + 1 d x = ∫ 1 - 1 x 2 + 1 d x = ∫ d x - ∫ 1 x 2 + 1 d x = x - tan - 1 ⁡ x

∫ 0 2,174 x 2 x 2 + 1 d x = x - tan - 1 ⁡ x 2,174 0 = 1,034

Só uma observação! Quando estiver calculando tan - 1 ⁡ 2,174 lembre de passar sua calculadora para radianos. Aperta a tecla mode!

tan - 1 ⁡ 2,174 ≈ 1.140

Vamos para o cálculo de V , apenas substituindo os valores que calculamos nas integrais acima!

V = 2 π ∫ 0 2,174 x 2 x 2 + 1 d x - ∫ 0 2,174 ( x 3 - 2 x 2 ) d x = 2 π 1,034 - - 1,264 = 14,438

Resposta

V ≈ 14,438

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método das cascas cilíndricas para achar o volume gerado pela rotação ao redor do eixo y da região limitada pelas curvas dadas. Esboce a região e a casca típica. y = 3 + 2 x - x 2 , x + y = 3
Use o método das cascas cilíndricas para achar o volume gerado pela rotação ao redor do eixo y da região limitada pelas curvas dadas. Esboce a região e a casca típica. y = 4 x - 2 2 , y = x 2 - 4 x +
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região limitada pelas curvas dadas ao redor dos eixos especificados. Esboce a região e a casca típica. y = x 2 , y = 0 ,
Use um gráfico para estimar as coordenadas de x dos pontos de interseção das curvas dadas. Então use essa informação para estimar o volume do solido obtido pela rotação ao redor do eixo y da região li
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região limitada pelas curvas dadas ao redor dos eixos especificados. Esboce a região e a casca típica. y = x - 1 , y = 0