33-34 Use o gráfico para estimar a abscissa dos pontos de inteerseção das curvas dadas. Então use essa informação e sua calculadora para estimar o volume do solido obtido pela rotação sobre o eixo da regição fechada sobre essas curvas.

33. ,

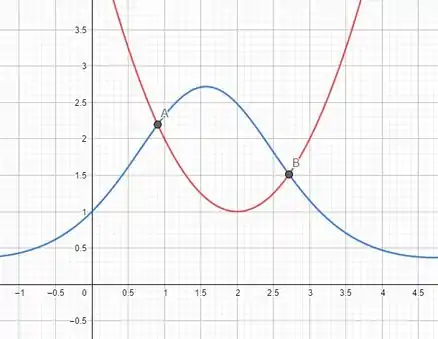
Em vermelho, é a nossa parábola

.

Em azul, é a função

E os ponto de encontros é são o ponto A e B, vou colocar com três casa decimais as abscissas, acredito que seja um bom valor. O ponto A tem abscissa igual a: e o ponto B tem abscissa igual a: 2,715

Porém, temos um inconveniente na hora de resolver a função (. Como temos que estimar o volume, iremos encontrar uma função mais simples no geogebra que tenha o gráfico parecido com a da função.

Usando o geogebra mais uma vez, conseguimos construir uma função que se assemelha a . No intervalo.

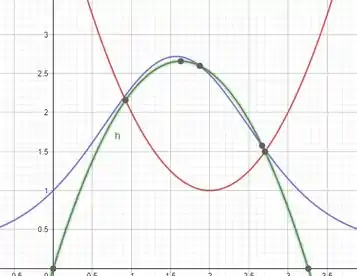
Que é a parábola que está em verde!!

vai virar

Então, o volume da região fechada em torno de é dada por:

Vamos resolver essa integral:

Resolveremos uma de cada vez, vamos para a mais fácil que é

Lembrando que estimamos tanto os pontos de encontra quanto a outra função, então esse valor do volume é aproximado!