Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.7 - Ex. 18
Calcular o volume do sólido gerado pela rotação, em torno da reta , da região limitada por , , e
Passo 1
Inicialmente vamos fazer uma ilustração para entender qual é a região delimitada pelas curvas. Se liga nessa ilustração:
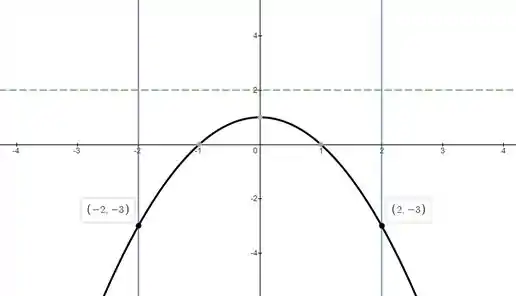
Analisando a figura acima, podemos ver que vamos integrar entre os pontos e .
Passo 2
Como queremos calcular o volume do solido gerado pela rotação da curva em torno do eixo :
Substituindo com o que achamos no Passo 1:
Isto é,
Abrindo esse termo ao quadrado:
Integrando:
Passo 3
Pra finalizar, vamos aplicar entre esses pontos.
Fazendo as contas:
Portanto,
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo dado. A região é a região, no primeiro quadrante, limitada acima pela curva y = x 2 , abaixo pelo eixo x e à direita p
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo dado. A região é a região, no segundo quadrante, limitada acima pela curva y = - x 3 , abaixo pelo eixo x e à esquerda
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Determine o volume do sólido obtido com a rotação da região limitada por y = 2 x , y = 0 e pelas retas x = 1 em torno Da reta x = 1 .Da reta x = 2 .
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .