Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.6 - Ex. 34

Verifique as afirmações e fórmulas nos Exercícios 33 e 34.

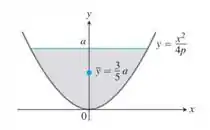
34 - Seja qual for o valor de p   >   0 na equação y   = x 2   4 p     , a ordenada do centroide do segmento parabólico mostrado aqui é y   =   3 5 a .

Passo 1

Aplicando a analogia utilizada no Exercício 1, onde foi encontrado que: x - = 0 . A faixa vertival típica tem o centro de massa:

x ~ , y ~ = x , a + x 2 4 p 2 , comprimento = a - x 2 4 p , largura = d x e área = d A = a - x 2 4 p     d x .

Massa = d m = δ   d A

Desta forma:

δ a - x 2 4 p   d x

Passo 2

Achar M x =   ∫ y ~   d m

M x = ∫ - 2 p a 2 p a 1 2 a + x 2 4 p a - x 2 4 p δ d x

M x = δ 2 ∫ - 2 p a 2 p a a + x 2 4 p a - x 2 4 p d x

M x = δ 2 ∫ - 2 p a 2 p a a 2 - x 4 16 p 2 d x

Resolvendo a integral, teremos:

M x = δ 2 a 2 x - x 5 80 p 2 - 2 p a 2 p a

M x = δ 2 a 2 ( 2 p a ) - 2 p a 5 80 p 2 - a 2 ( - 2 p a ) - - 2 p a 5 80 p 2

M x = δ 2 2 a 2 p a - 2 5 ⋅ a 2 ⋅ p 2 p a 80 p 2 - - 2 a 2 p a + 2 5 ⋅ a 2 ⋅ p 2 p a 80 p 2  

M x = δ 2 2 a 2 p a - 32 a 2 p a 80 - - 2 a 2 p a + 32 a 2 p a 80

M x = δ 2 2 a 2 p a - 2 a 2 p a 5 - - 2 a 2 p a + 2 a 2 p a 5  

M x = δ 2 10 a 2 p a - 2 a 2 p a 5 - - 10 a 2 p a + 2 a 2 p a 5

M x = δ 2 10 a 2 p a - 2 a 2 p a 5 + 10 a 2 p a - 2 a 2 p a 5

M x = δ 2 2 10 a 2 p a - 2 a 2 p a 5

M x = δ 10 a 2 p a - 2 a 2 p a 5 = δ 8 a 2 p a 5

Deste modo:

M x = 8 a 2 δ p a 5

Passo 3

Achar M:

M =   ∫ d m =   ∫ - 2 p a 2 p a δ a - x 2 4 p d x

M = δ ∫ - 2 p a 2 p a a - x 2 4 p d x

Resolvendo a integral teremos:

M = δ a x - x 3 12 p - 2 p a 2 p a

M = δ a ( 2 p a ) - 2 p a 3 12 p - a ( - 2 p a ) - - 2 p a 3 12 p

M = δ 2 a p a - 8 p a p a 12 p - - 2 a p a + 8 p a p a 12 p

M = δ 2 a p a - 8 a p a 12 - - 2 a p a + 8 a p a 12  

M = δ 24 a p a - 8 a p a 12 + 24 a p a - 8 a p a 12

M = δ 2 24 a p a - 8 a p a 12

M = 2 δ 16 a p a 12

M = 2 δ 8 a p a 6 = δ 8 a p a 3 = 8 a δ p a 3

Passo 4

Achar y - = M x M

y - = 8 a 2 δ p a 5 8 a δ p a 3

y - = 8 a 2 δ p a 5 ⋅ 3 8 a δ p a

y - = 3 a 5

Resposta

Logo a o centro será:

y - = 3 a 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ - 1 1 ( 1 - y 2 )d y
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região. y = 1 - x 2 ,y = 0 ; e mt o r n od oe i x ox
Encontre uma integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas sobre a reta especificada. Em seguida, use a calculadora para determinar a integral com precis
Encontre uma integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas sobre a reta especificada. Em seguida, use a calculadora para determinar a integral com precis
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região. y = 1 4 x 2 ,y = 5 - x 2 ; e mt o r n od oe i x ox