36. Utilize uma ferramenta gráfica como no Exemplo 4 (ou o Método de Newton ou um determinador de raízes) para encontrar os pontos críticos de com precisão de três casas decimais. Em seguida, classifique o ponto crítico e determine o valor mais alto e o mais baixo do gráfico.

é um quadrilátero cujos vértices são:

Agora vamos montar o quadrilátero que ele fala do enunciado, olha só:

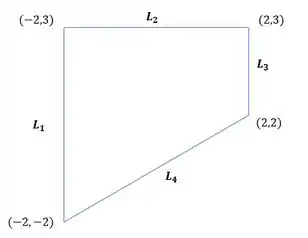
Como podemos ver, apenas e estão dentro do quadrilátero . Portanto, apenas esses pontos podem ser pontos críticos.

Para o ponto :

E para o ponto :

Mas tem um Teorema que nos diz o seguinte: Os pontos de máximos e mínimos absolutos podem ocorrer apenas nos pontos críticos que estão dentro da região ou em algum ponto na “borda” da região .

Primeiro vamos ver em

Logo,

Então vamos checar a fronteirada região . Como vamos analisar os limites da região , vamos olhar para:

:

:

Agora vamos olhar para os pontos críticos. Derivando, temos:

Assim,

Se

Se

Agora vamos olhar para

Logo,

para

Analisando a fronteira:

:

:

Agora vamos ver os pontos críticos. Derivando:

Igualando a zero, chegamos em:

Considerando ,

Considerando ,

Em

Logo,

Analisando a fronteira:

:

:

Derivando para achar os pontos críticos:

Igualando a zero:

Como , podemos descartar o caso em que Assim,

Para :

Por fim, vamos analisar

Assim,

Analisando a fronteira, temos o seguinte:

Em :

Em :

Pra finalizar, vamos olhar para os pontos críticos.

Derivando,

Portanto, vemos que nunca será zero. Assim, não há candidatos aos pontos críticos.

Analisando os pontos críticos, temos:

Assim, o valor máximo ocorre para os pontos e e o máximo absoluto é . Já o mínimo, ocorre apenas para o ponto e o mínimo absoluto é .