Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.9 - Ex. 37
37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?
Passo 1
Vamos seguir os seguintes passos para resolver qualquer questão de taxas:
- Leia cuidadosamente o problema.
- Se possível, faça um diagrama.
- Indentificar as variáveis e as constantes do problema.
- Escreva uma equação que relacione as variáveis.
- Derive em ambos os lados em relação a t usando regra da cadeia.
- Substituir o que foi dado e encontrar o que foi pedido.
Se liga na ilustração do que a questão disse:
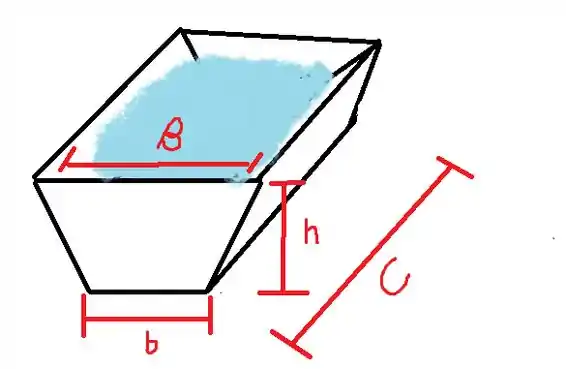
Primeiro, tina é esse recibiente ai onde coloca água.
Vamos anotar as variáveis desse problema:
C o comprimento da tina.
base menor da face trapezoidal da tina.
B Base maior da face trapezoidal da tina.
h- altura da face trapezoidal da tina.
A questão nos deu:
C=16
h =4
b=4
B =6
E nos pede para entramos a taxa da altura da água, , quando h for igual a 3.
Passo 2
Iremos usar a fórmula do volume para resolver essa questão, lembrando que o volume de um sólido é dado pela área da base(no nosso caso a parte trapezoidal) vezes o comprimento.
Temos duas variáveis aqui, , mas não temos nenhuma informação de , então, teremos que reescrever está variável em função de outras variáveis.
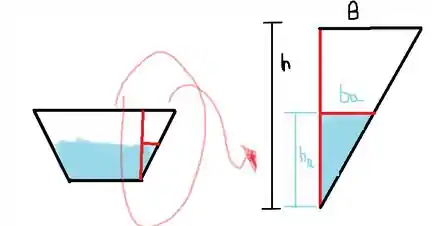
Na imagem mostrada é possível usar semelhança de triângulos:
Além disso, B=1, pois vamos pensar um pouco, toda a base trapezoidal vale 6, se você diminuir por 4 da base menor, sobra só 2,ou seja, 1m para cada canto.
Passo 3
Já ilustramos o que a questão pediu, já encontramos a equação que descreve o problema, agora só falta derivar.
Derivando em ambos os lados em relação a t:
Substituindo o que encontramos: