Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 9

Seja θ (em radianos) um ângulo agudo de um triângulo retâgulo, e sejam x e y , respectivamente, os comprimentos dos lados adjacente e oposto a θ . Suponha, também, que x e y variem com o tempo.

(a) Como se relacionam d θ d t , d x d t e d y d t ?

(b) Em um certo instante, x   =   2   u n i d a d e s e está crescendo 1   u n i d a d e / s , enquanto y   =   2   u n i d a d e s e está decrescendo 1 4   u n i d a d e / s . Com que rapidez θ estará variando naquele instante? θ está crescendo ou decrescendo naquele instante?

Passo 1

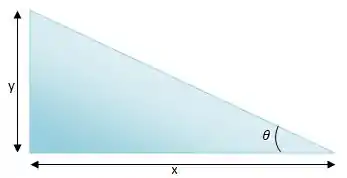
Para relacionar x ,   y   e θ podemos aplicar a definição de tangente:

t a n g e n t e =     c a t e t o   o p o s t o c a t e t o   a d j a c e n t e               ⇒                 tan ⁡ θ = y x

Passo 2

(a)

Para relacionar d θ d t , d x d t e d y d t , podemos derivar essa expressão da tangente em relação ao tempo:

tan ⁡ θ = y x     ⇒     x tan ⁡ θ = y

d d t ( x tan ⁡ θ ) = d y d t

Usando a Regra do Produto, temos:

d x d t tan ⁡ θ + x d ( tan ⁡ θ ) d t = d y d t

Como x e y variam com o tempo, θ também vai variar. Então derivando e sem esquecer da regra da cadeira vamos chegar no seguinte:

d x d t tan ⁡ θ + x ( tan ⁡ θ ) ' d ( θ ) d t = d y d t

d x d t tan ⁡ θ + x sec ⁡   θ 2   d ( θ ) d t = d y d t

Organizando melhor vamos chegar na expressão que relaciona   d θ d t , d x d t e d y d t

Usando que sec ⁡ θ 2 = 1 cos ⁡ θ 2

x ( cos ⁡ θ ) 2   d θ     d t     =     d y d t - tan ⁡ θ d x d t

d θ d t     =     cos ⁡ θ   2 x d y d t - tan ⁡ θ d x d t

Mas tan ⁡ θ = y x , lembra?

d θ d t     =     cos ⁡ θ   2 x d y d t - y x d x d t

Finalmente chegamos em:

d θ d t     =     cos ⁡ θ   2 x 2   x d y d t - y d x d t

Passo 3

(b)

Nesse enunciado ele dá alguns dados pra gente, vamos ver quais são eles:

x   =   2 u n i d a d e s e crescendo 1   u n i d a d e / s , então d x d t = 1

y   =   2   u n i d a d e s e decrescendo 1 4 u n i d a d e s ,   e n t ã o     d y d t =   - 1 4 . Lembrando de atentar pro sinal negativo por estar decrescendo.

Além disso, se x = 2 e y = 2 , então:

tan ⁡ θ = y x = 2 2 = 1         ⇒       θ = π 4

cos ⁡ θ = cos ⁡ π 4 =   2 2

Substituindo todos esses dados na expressão que encontramos na letra (b), ficamos com:

d θ d t     =     cos ⁡ θ   2 x 2   x d y d t - y d x d t

d θ d t     =     2 2   2 2 2   2 - 1 4 - ( 2 ) ( 1 )

d θ d t     =     1 8   2 - 1 4 - ( 2 ) ( 1 )

d θ d t     =     1 4   - 1 4 - 1

d θ d t     =     1 4   - 5 4   =   - 5 16   r a d / s

Como d θ d t < 0 , isso significa que naquele instante θ   está decrescendo.

Resposta

(a) d θ d t     =     cos ⁡ θ   2 x 2   x d y d t - y d x d t

(b)   d θ d t =   - 5 16   r a d / s , θ está decrescendo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

34. A medida de um ângulo agudo de um triângulo retângulo está decrescendo a uma taxa de 1 36 π rad/s. Se o comprimento da hipotenusa for constante e igual a 40cm, ache a velocidade com que a área est
37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?
39. O volume de um balão está decrescendo a uma taxa proporcional à sua área superficial. Mostre que o raio do balão diminui a uma taxa constante.
Uma viga com 30m de comprimento está apoiada em uma parede e o seu topo está se deslocando para baixo a uma velocidade de 0,5m / s . Qual será a taxa de variação de medida do ângulo formado pela viga
38. Uma escada com 7m de comprimento está apoiada numa parede. Se o pé da escada for empurrado horizontalmente em direção à parede a 1,5m/s, com que velocidade o topo da escada será deslocado para cim