Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 25

Um tanque de água cônico com o vértice para baixo tem um raio de 10   m no topo e uma altura de 24   m . Se a água fluir dentro do tanque a uma taxa de 20   m 3 / m i n , com que velocidade sua profundidade estará crescendo quando ela tiver 16   m de profundidade?

Passo 1

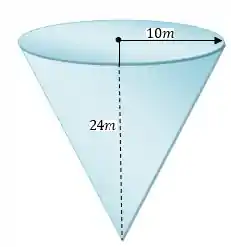
Para relacionar a altura desse cone com o raio da base podemos usar a fórmula de volume do cone:

V = 1 3   π R 2 h

Mas tem água sendo despejada aí dentro ne? Então vamos falar que num momento qualquer a profundidade da água, ou seja, a distância entre o vértice do cone até a superfície da água, é h . E o raio desse novo cone formado pela água é r .

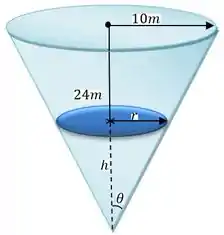
Então vamos falar que o volume ocupado pela água num instante qualquer é

V = 1 3   π r 2 h

Além disso podemos falar que:

tan ⁡ θ = 10 24 = r h

Passo 2

Como o enunciado pede pra gente a velocidade com que a profundidade da água estará crescendo, basta encontrarmos d h / d t

Pra esse cara aparecer, vamos derivar em relação ao tempo a expressão de volume:

d V d t   = d d t 1 3   π r 2 h = π 3 d r 2 h d t  

Usando a regra da derivada do produto, vamos ter:

d V d t   = π 3 d r 2 d t   h + r 2   d h d t

Pela regra da cadeia:

d V d t   = π 3 d r 2 d r d r d t     h + r 2   d h d t

d V d t   = π 3 2 r h d r d t + r 2   d h d t

Chegamos que

d V d t   = π r 3 2 h d r d t + r   d h d t                         e q u a ç ã o   ( 1 )

Passo 3

Mas aí apareceu o d r / d t que não temos, mas podemos derivar a tangente pra relacionar ele com d h d t

tan ⁡ θ = r h       ⇒     h tan ⁡ θ = r

d d t h tan ⁡ θ = d r d t

Como o ângulo θ não varia:

tan ⁡ θ   d h d t = d r d t

E tan ⁡ θ = 10 24 = 5 12

5 12 d h d t = d r d t                     e q u a ç ã o   ( 2 )

Passo 4

No instante que ele fala a água flui para dentro do tanque a uma taxa de 20   m 3 / m i n , ou seja

d V d t = 20   m 3 / m i n  

E como o enunciado fala da água a 16   m   d e   p r o f u n d i d a d e , h = 16 m . E aí usando que

tan ⁡ θ = 10 24 = r h

r = 16 10 24         ⇒       r = 20 3

Passo 5

Agora partiu relacionar as equações (1) e (2)?

d V d t   = π r 3 2 h d r d t + r   d h d t                         e q u a ç ã o   ( 1 )

5 12 d h d t = d r d t                                                                     e q u a ç ã o   2

Substituindo (2) em (1):

d V d t   = π r 3 2 h 5 12 d h d t + r   d h d t

d V d t   = π r 3 d h d t 2 h 5 12 + r  

Substituindo

d V d t = 20   m 3 / m i n  

r = 20 3

h = 16 m

Fica assim:

d V d t   = π r 3 d h d t 2 h 5 12 + r  

20   = π 20 3 3 d h d t 2 ( 16 ) 5 12 + 20 3

Aí partiu fazer essas continhas

20   = 20 π 9 d h d t 4 0 3 + 20 3

1   = π 9 d h d t 6 0 3

1   = π 9 d h d t 20

d h d t = 9 20 π m / m i n

E como a velocidade com que a profundidade da água cresce é basicamente d h / d t . Encontrarmos nossa resposta 😊

Resposta

9 20 π m / m i n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11- Se o comprimento original x do lado de um cubo de 24 m diminui a taxa de 5m / m i n quando x = 3 , a que taxab) o volume do cubo varia?
4- Suponha que 2 x + 3 y = 12 e d y d t = - 2 . Determine d x d t .
12- A área da superfície de um cubo aumenta a taxa de 72 p o l 2 / s . A que taxa o volume do cubo varia quando o comprimento do lado é de x = 3p o l ?
9- Se L = x 2 + y 2 , d x d t = - 1 e d y d t = 3 , determine d L d t quando x = 5 e y = 12 .
1-Área Suponha que o raio r e área A = π r 2 de um círculo sejam deriváveis de t. Escreva uma equação que relacione d A / d t a d r / d t .