Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 23
Um satélite está em uma órbita elíptica em torno da Terra. A sua distância (em milhas) do centro da Terra é dada por
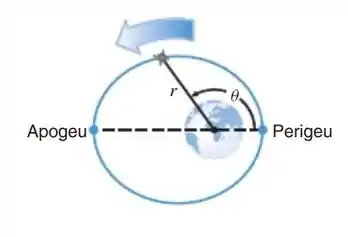
Onde é o ângulo medido do ponto da órbita mais próximo da superfície da Terra (veja a figura abaixo).
(a) Encontre a altitude do satélite no perigeu (ponto mais próximo da superfície da Terra) e no apogeu (ponto mais distante da superfície da Terra) usando como o raio da Terra.
(b) No instante em que for o ângulo está crescendo a uma taxa de . Encontre a altitude do satélite e a taxa segundo a qual a altitude estará variando naquele. Expresse a taxa em unidades de .
Passo 1
(a)
No Perigeu . Colocando na fórmula:
A distância até a superfície da terra a distância até o centro menos o raio da terra concorda?
Então chamando a altitude no perigeu de e o raio da terra de
No Apogeu . Colocando na fórmula:
E agora usando que é a altitude do satélite no apogeu:
Passo 2
Para . Colocando na fórmula:
Para achar
Passo 3
Para a segunda parte da letra (b) vamos derivar em relação ao tempo a expressão que o enunciado nos dá:
Pela regra da cadeia:
O enunciado fala que e que ângulo está crescendo a uma taxa de , então:
Substituindo esses dados todos na expressão que a gente encontrou:
Passo 4
Mas queremos a taxa com que a altitude está variando, então vamos derivar a seguinte expressão:
Então
Resposta
ℎ𝑝
(a)
(b)