Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 37
37. Na ilustração 1 temos a função valor absoluto definida por e essa função não é derivável em 0. Prove que para todo . (Sugestão: seja .
Passo 1
Primeiramente, devemos perceber que o enunciado nos traz um erro. A partir daí, para encontrar o resultado basta utilizarmos a definição de derivada e a sugestão fornecida pelo enunciado.
Passo 2
Sabemos que 
.
Passo 3
Da definição de derivada, temos :
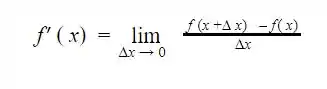
Passo 4
Como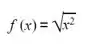 
. Substituindo na definição de derivada temos:
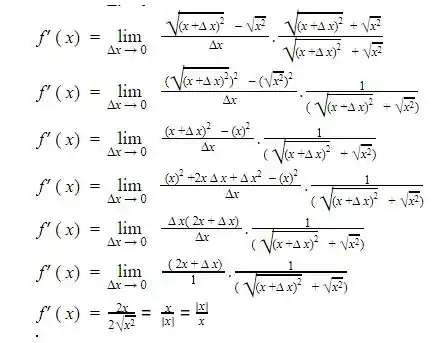
Resposta
Demonstração.
Exercícios de Livros Relacionados
Suponha que g x = f x . Se f n ( x ) existir e f x ≠ 0 , prove que g n x = f x f xf n ( x )
Dê um exemplo de duas funções f e g , tais que f não seja derivável em g ( 0 ) , g seja derivável em 0 e f ∘ g seja derivável em 0 .
No exercício 61 dos exercícios 3.1 você provou que se f for derivável em a , então f ' a = lim Δ x → 0 f a + Δ x - f ( a - Δ x ) 2Δ x Mostre, usando a função valor absoluto, que é possível existir o
Sejam f e g funções cujos domínios são o conjunto de todos os números reais. Além disso, suponha que (i) g x = x f x + 1 ; (ii) g a + b = g a ⋅ g ( b ) para todo a e b ; (iii) lim x → 0 f ( x ) = 1
Se f ' ( x 1 ) existir, prove que lim x → x 1 x f x 1 - x 1 f ( x ) x - x 1 = f x 1 - x 1 f ' ( x 1 )