Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 4.2 - Ex. 3b

3-Encontre o máximo e mínimo absoluto de cada uma das seguintes funções:

b) f x ,   y = x 3 + y 3 - 3 x y ,   na região triangular de vértices   0 ,   0 ,   0 ,   1   e   1 ,   0 .

Passo 1

Galera, a primeira coisa que temos que fazer é encontrar os pontos críticos dessa função. Para identificar esses pontos temos que resolver o seguinte sistema:

∂ f ∂ x = 0  

∂ f ∂ y = 0  

Ou seja, as derivadas parciais da função z   =   f ( x , y ) tem que ser iguais a zero.

Nesse caso não é só isso. Podemos também ter pontos críticos na fronteira da nossa região e estes, podem ser extremos absolutos. Aqui, temos a seguinte região:

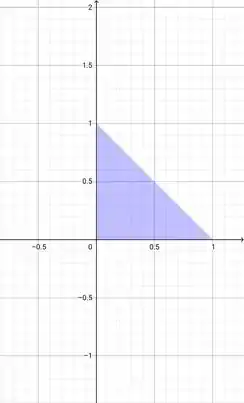
Passo 2

Dessa forma, temos que:

∂ f ∂ x = 3 x 2 - 3 y

∂ f ∂ y = 3 y 2 - 3 x

Assim,

3 x 2 - 3 y = 0 3 y 2 - 3 x = 0

Da primeira equação podemos tirar isso aqui:

3 x 2 = 3 y

y = x 2

Substituindo isso na segunda equação:

3 x 2 2 - 3 x = 0

3 x 4 - 3 x = 0

x   3 x 3 - 3 = 0

x = 0

E

x 3 = 1

x = 1

Para x = 0 :

y = 0

Para x = 1 :

y = 1

Achamos os seguintes pontos críticos: ( 0 ,   0 ) e ( 1,1 ) , mas podem existir outros. Ainda temos que verificar os pontos que podem haver na fronteira da nossa região.

Passo 3

-Segmento de reta entre ( 0,0 ) e 1 ,   0 : Nesse segmento de reta, temos y = 0 , portanto, podemos simplificar a nossa função para uma única variável:

u x = x 3 ,           0 ≤ x ≤ 1

Derivando u ( x ) e igualando a zero:

u ´ x = 3 x 2 = 0

x = 0

Temos o ponto 0,0 .

-Segmento de reta entre ( 0,0 ) e 0,1 : Nesse segmento de reta, temos x = 0 , portanto, podemos simplificar a nossa função para uma única variável:

s ( x ) = y 3 ,           0 ≤ y ≤ 1

Derivando s ( x ) e igualando a zero:

s ´ x = 3 y 2 = 0

y = 0

Temos o ponto 0,0 .

-O segmento de reta entre ( 0,1 ) e ( 1 ,   0 ) : No plano x y , uma equação para esse segmento é

y = - x + 1 ,           0 ≤ x ≤ 1

Substituindo isso na nossa função temos w x :

w x = x 3 + - x + 1 3 - 3 x ( - x + 1 )

Derivando a nossa nova função:

w ´ x = 3 x 2 - 3 - x + 1 2 - 3 - x + 1 + 3 x

Desenrolando essa tranqueira, temos:

w ´ x = 3 x 2 - 3 x 2 - 2 x + 1 + 3 x - 3 + 3 x

w ´ x = 12 x - 6

Igualando a zero:

12 x - 6 = 0

x = 1 2

Obtemos então, o seguinte ponto:

1 2 , 1 2

Passo 4

Estes são todos os pontos críticos que encontramos:

0,0 ,   1,1 ,   1 2 , 1 2

Também temos os pontos de fronteira, nos quais podem ocorrer extremos absolutos:

0,0 ,   0,1 ,   ( 1,0 )

Cara, nós temos que desconsiderar o ( 1,1 ) porque ele não está na nossa região. No total temos 5 pontos. Para sabermos qual desses pontos tem valor máximo e qual possui valor mínimo, vamos testá-los na nossa função.

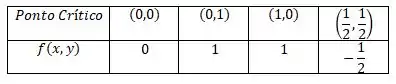
Resposta

Máximo absoluto igual a 1 em 0,1 , 1,0 .   Mínimo absoluto igual a - 1 2 em 1 2 , 1 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores máximo e mínimo absolutos de f no conjunto D .33. f x , y = x 4 + y 4 - 4 x y + 2 . D = { ( x , y ) | 0 ≤ x ≤ 3 ,0 ≤ y ≤ 2 }
Determine os valores máximo e mínimo absolutos de f no conjunto D . f x , y = x y 2 , D = x , y x ≥ 0 , y ≥ 0 ,x 2 + y 2 ≤ 3
Determine os valores máximos e mínimo absolutos de f no conjunto D. f x , y = 3 + y x - x - 2 y , D é a região triangular fechada com vértices 1 , 0 ,5 , 0e1 , 4
36. Utilize uma ferramenta gráfica como no Exemplo 4 (ou o Método de Newton ou um determinador de raízes) para encontrar os pontos críticos de f com precisão de três casas decimais. Em seguida, classi