Determine os valores máximo e mínimo absolutos de no conjunto .
Passo 1
Fala aí! tudo certinho?
Neste exercício, queremos encontrar os pontos onde a função 𝑓 tem o maior e o menor valor no conjunto 𝐷, onde e são dados por:
A função 𝑓 depende de duas variáveis, 𝑥 e 𝑦, e o conjunto 𝐷 é formado por todos os pares de números não negativos (𝑥,𝑦) que satisfazem a condição . Isso significa que o conjunto 𝐷 é uma região do plano limitada por uma curva.
Como vamos resolver isso?
Primeiro, vamos analisar a função 𝑓 e o conjunto 𝐷 e ver se eles têm alguma propriedade ou simetria que possa nos ajudar.
Depois, vamos usar o método de teste da derivada para encontrar os pontos críticos de 𝑓 dentro de 𝐷 e na fronteira de 𝐷. Ou seja, fazemos:
Derivamos em relação a considerando constante e vice-versa.
Por fim, vamos comparar os valores de 𝑓 nesses pontos e determinar qual é o máximo e qual é o mínimo absoluto.
Veja só!
Passo 2
Vamos começar calculando as derivadas parciais:
Pela regra da potencia, temos:
Agora pelo teste da derivada igualamos ambas as derivadas a .
Se :
Se :
Então ou ou . Logo não há ponto crítico no interior de .
Podemos esboçar a região lembrando que é um circulo de raio :
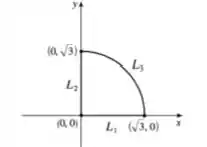
Tranquilo até aqui?
Passo 3
Então só nos resta analisar a função nos limites da região:
Em , :
Em :
Em , :
Pegando
Para
Logo, aplicando o teste da derivada derivando e igualando a , temos:
Calculando a imagem da função em ...
Comparando as imagens que calculamos nesse passo, temos:
O valor máximo é e o valor mínimo absoluto é , que ocorre em .
Assim, o máximo absoluto de em é e o mínimo absoluto é, que ocorre em todos os pontos de e .
É isso! O que achou? Responde Aí!
Resposta
O máximo absoluto de em é e o mínimo absoluto é, que ocorre em todos os pontos de e .