Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 39
39. A Região limitada pela curva e pelas retas é girada em torno do eixo x. Ache o volume do sólido gerado.
Passo 1
Antes de tudo, vamos esboçar essas curvas,
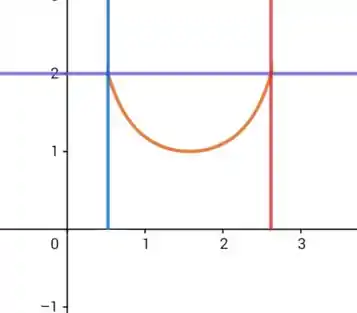
Em azul: .
Em vermelho:
Em roxo: y=2
Em marrom:
Agora vamos gerar o sólido de revolução em torno do eixo x.
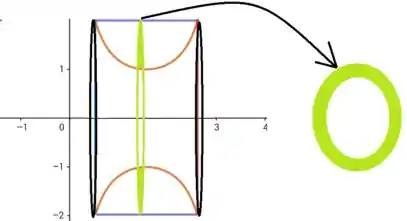
Nessa imagem, giramos as curvas em torno do eixo e fatiamos um pedaço do sólido, obtendo assim um anel.
Passo 2
A área do anel que desejamos é dado pela área com o raio maior menos a área do raio menor, ou seja,
Passo 3
A integral ficará assim:
Lembrando que x está variando de -1/2 a 1, por isso que esses são os limites da integral.
Resolvendo a integral:
Resposta
Exercícios de Livros Relacionados
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 3 em torno de O A .
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = x + 1 ,y = 0 , x = 0 , x = 2 ;
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. x = 2 - y 2 , x = y 4 s o b r eoe
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = x 3 , y = 1 ,x = 2 s o b r ey
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = e x ,y = 0 , x = - 1 , x = 1 s