Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.7 - Ex. 4

4. y = cos x , y = sen x , x = 0 e x = (pi)/(4)

Passo 1

Temos que encontrar o volume do sólido através da rotação da região delimitada pelas curvas em torno do eixo x:

y = cos x e y = sen x

O gráfico dessa equação é o seguinte:

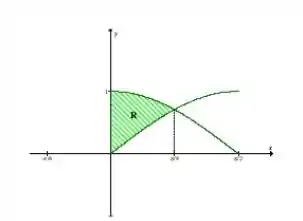
Passo 2

A área de seção transversal é A (x) = pi (c o s x)^2 - pi ( sen x )^2

Para obtermos o volume gerado pela revolução de R em torno do eixo x, usaremos a seguinte fórmula:

V = pi int_a^b A ( x ) d x

Portanto, o volume é:

V = pi int_o^((pi)/(4)) ( cos^2 x - sen^2 x ) d x

= pi int_o^((pi)/(4)) ( cos^2 x - sen^2 x ) d x

= pi int_o^((pi)/(4)) ((1 + cos 2 x)/(2) - (1 - cos 2 x)/(2)) d x

Simplificando, temos

= pi int_o^((pi)/(4)) c o s (2 x) d x

= ((pi)/(2) ( sen 2 x )|_0^((pi)/(4))

= (pi)/(2) u . v

Resposta

= (pi)/(2) u . v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x Região, no primeiro quadrante, limitada acima pela reta y = 2 . Abaixo pela curva y =
36 - Use um teorema de Pappus para determinar o volume gerado pela rotação em torno da reta x=5 da região triangular delimitada pelos eixos coordenados e pela reta 2 x + y=6 .
Verifique as afirmações e fórmulas nos Exercícios 33 e 34.33 - As coordenadas do centroide de uma curva plana derivável são:
45 - Nos Exercícios 45 e 46, use um teorema de Pappus para determinar o centroide do triângulo dado. Use o fato de que o volume de um cone de raio r e altura h é V = 1 3 π r 2 h .
Verifique as afirmações e fórmulas nos Exercícios 33 e 34.34 - Seja qual for o valor de p0 na equação y= x 24 p , a ordenada do centroide do segmento parabólico mostrado aqui é y=3 5 a .