Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.4 - Ex. 41
41. a) Encontre os valores de e na figura a seguir.
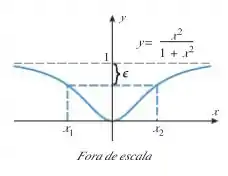
b) Encontre um número positivo , tal que:
Com .
c) Encontre um número negativo , tal que:
Com .
Passo 1
a) Então galera, aqui não possui muito segredo não, ok? O valor da função correspondente aos pontos e é . Sabendo disso, teremos que para :
Isolando :
E como, observando o gráfico, , podemos dizer que:
E esses são os valores de e , galeris!
Passo 2
b) Temos a seguinte desigualdade, pessoal:
Isolando , teremos:
Mas como , comparando temos:
Passo 3
c) Temos a seguinte desigualdade, pessoal:
Aqui temos que seguir exatamente os mesmos passos da letra b), pessoal! A diferença aqui é que , dessa forma, teremos que será o oposto do que achamos na letra b), ou seja:
E estão aí nossas respostas, pessoal!
Resposta
a)
b)
c)
Exercícios de Livros Relacionados
Esboce o gráfico de um exemplo de função f que satisfaça todas as condições dadas. lim x → 1 - f ( x ) = 2lim x → 1 + f x = - 2 f 1 = 2
Esboce o gráfico de um exemplo de função f que satisfaça todas as condições dadas. lim x → 0 - f x = 2lim x → 0 + f x = 0 lim x → 4 - f x = 3 lim x → 4 + f x = 0 f 0 = 2f 4 = 1
Use uma tabela de valores para estimar o valor do limite. Caso tenha um dispositivo de gráficos, usar para confirmar o resultado. lim θ → 0 sin 3 θ tan 2 θ
Esboce o gráfico de um exemplo de função f que satisfaça todas as condições dadas. lim x → 3 + f x = 4 lim x → 3 - f x = 2lim x → - 2 f x = 2 f 3 = 3f - 2 = 1
Esboce o gráfico de um exemplo de função f que satisfaça todas as condições dadas. lim x → 0 - f x = 1lim x → 0 + f x = - 1lim x → 2 - f x = 0 lim x → 2 + f ( x ) = 1f 2 = 1f 0n ã oe s t ád e