Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 18
Esboce o gráfico de um exemplo de função que satisfaça todas as condições dadas.
Passo 1
Bom pessoal, vamos aos limites!
Queremos um gráfico com as características que ele dá no enunciado, então primeiro, vamos entender cada uma delas:
- Isto quer dizer que quando se aproxima do eixo da esquerda pra direita, tende ao valor 2.
- Isto quer dizer que quando se aproxima do eixo da direita pra esquerda, tende ao valor 0.
- Isto quer dizer que quando o se aproxima do valor 4 da esquerda para a direita, tende ao valor 3.
- Isto quer dizer que quando o se aproxima do valor 4 da direita para a esquerda, tende ao valor 0.
- E temos também 2 pontos definidos da função: e
- quando se aproxima do eixo pela esquerda , tende a 2.
- quando se aproxima do eixo pela direita, tende a 0.
- quando se aproxima de 4 pela esquerda, tende a 3.
- quando se aproxima de 4 pela direita, tende a 0.
Agora vamos ver como essas informações se combinam no passo 2.
Passo 2
Essas duas informações nos dizem que no ponto temos uma descontinuidade. Os limites laterais são diferentes e a função vai ter um salto.
A mesma conclusão pode ser tirada do ponto . Os limites laterais são diferentes e temos uma descontinuidade.
Ta mais que curvas são essas? A gente só tem limites, não tem nenhuma função.
Pois é, você pode escolher quaisquer curvas, desde que os limites dados pelo enunciado sejam verdadeiros. Repara que o enunciado pediu UM EXEMPLO!
Passo 2
Então considerando as descontinuidades nos pontos e , podemos então esboçar a curva.
Lembrando que o valor da função nesses pontos é onde vamos preencher a bolinha no gráfico.
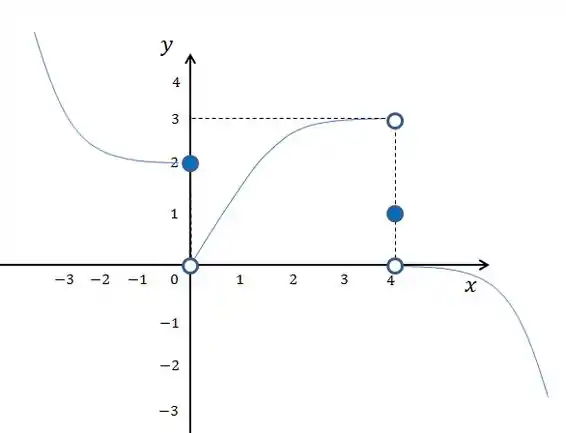
Resposta
