43-46 Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.
44-Com , o gráfico de fica abaixo do gráfico de e acima do gráfico de .
Passo 1
Galerinha, para resolvermos essa questão nós só temos que analisar o gráfico dessas três funções juntas. Olha só:
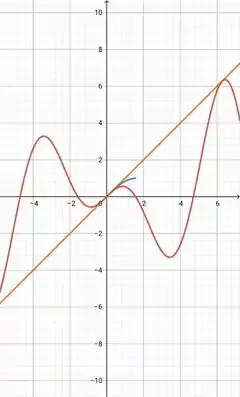
A função azul é a nossa função limitada . Já a função laranja é a nossa função . Por último, temos a função vermelha que é .
Dessa forma, podemos ver que o gráfico da nossa função está abaixo do gráfico da função laranja e acima daquele da função .
Portanto, a nossa afirmativa é verdadeira.
Resposta
Veradeira.