Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.2 - Ex. 44
A região limitada pelo eixo y e pelas curvas e para gira em torno do eixo x. Ache o volume do sólido de revolução gerado.
Passo 1
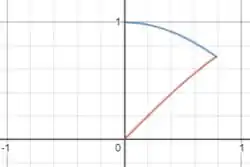
Vamos utilizar a imagem abaixo para visualizar melhor a região, a linha azul representa a curva pois quando x é zero cosseno é 1, e linha vermelha representa a curva :
Como vamos rotacionar a região, vamos precisar usar a equação de volume por anéis circulares:
Passo 2
Como deve ser a função mais distante do eixo de rotação, ela será e a será
Os limites de integração serão os extremos do intervalo . Nossa integral então será:
Passo 3
Agora vamos resolver a integral, pelas identidades trigonométricas:
Nossa integral fica:
Integrando:
Substituindo os limites:
Resposta
Exercícios de Livros Relacionados
55- Determinação de volume Determine o volume do sólido gerado pela rotação da região do primeiro quadrante delimitada pelos eixos coordenados e pela curva y = cos x ,0 ≤ x ≤ π / 2 , em tornoDa reta
54- Determinação de volume Determine o volume do sólido gerado pela rotação da região do primeiro quadrante delimitada pelos eixos coordenados, pela curva y = e - x e pela reta x = 1 .Em torno do eixo
56- Determinação de volume Determine o volume do sólido gerado pela rotação da região delimitada pelo eixo das abcissas e pela curva y = x s e nx , 0 ≤ x ≤ π , em tornoDo eixo das ordenadasVeja o gráf
53- Determinação do volume Determine o volume do sólido gerado pela rotação da região do primeiro quadrante delimitada pelos eixos coordenados, pela curva y = e x e pela reta x = ln 2 em torno da re
54- Determinação de volume Determine o volume do sólido gerado pela rotação da região do primeiro quadrante delimitada pelos eixos coordenados, pela curva y = e x e pela reta x = 1 .Em torno da reta x