48. Dois cilindros circulares retos, cada um tendo um raio de r unidades, têm seus eixos interceptando-se em ângulos retos. Ache o volume do sólido comum aos dois cilindros.

Não entendeu nadinha? Senta aí que você vai ver que não é tão difícil assim.

Ilustrando o que a questão pediu:

A esquerda os dois cilindros e a esquerda a região comum entre os dois.

Na intersecção dos dois cilindros é possível observar este quadrado:

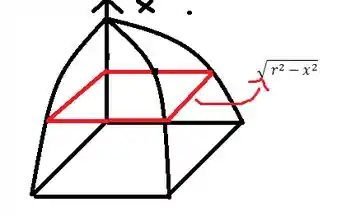
Que terá a área igual a .

Mas isso é só em um lado, para termos referente a todo o sólido teremos que multiplicar por 4.( referente as 4 faces laterais)