Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 71
Alguns dos pioneiros do cálculo, como Kepler e Newton, foram inspirados pelo problema de encontrar os volumes de barris de vinho. (De fato, Kepler publicou um livro em 1615, Stereometria doliorum, dedicado aos métodos para encontrar os volumes de barris.) Eles frequentemente aproximavam a forma dos lados por parábolas.
- Um barril com altura e raio máximo é construído pela rotação ao redor do eixo da parábola , , onde é uma constante positiva. Mostre que o raio de cada extremidade do barril é , onde .
- Mostre que o volume delimitado pelo barril é
Passo 1
Falaeee, belezinha?? Bom... a questão quer que demonstremos que o raio de cada extremidade do barril é , onde .
Para isso, a questão nos diz que o barril com altura e raio máximo é construído pela rotação ao redor do eixo da parábola , , onde é uma constante positiva.
Nesse sentido, podemos calcular o volume da seguinte forma:
Em seguida, a questão quer que mostremos que o volume delimitado pelo barril é dado por:
E aí?? Bora lá?? 😉
Passo 2
Para ficar melhor nossa visualização, vamos observar a figura abaixo:
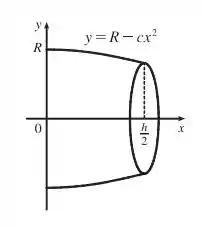
O raio do barril é o mesmo em cada extremidade por simetria, desde que a função seja a mesma.
Como o barril é obtido pela rotação do gráfico da função sobre o eixo , o raio é igual ao valor de em , que é .
Passo 3
O barril é simétrico sobre o eixo , então o volume é duas vezes da parte do barril para .
Além disso, o barril é o volume de uma rotação, então:
Passo 4
Tentando fazer com que pareça mais com a expressão que queremos, nós a reescrevemos como
Além disso, podemos reescrever a parte interior da seguinte forma:
Substituindo novamente em , temos que
Entendeu direitinho?? Responde aee!! 😉
Resposta
Demonstração