Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.Revisão - Ex. 48

48. Prove que o retângulo que tem a base no eixo e dois vértices na curva , terá a maior área possível se os seus vértices estiverem nos pontos de inflexão do gráfico.

Passo 1

Vamos desenhar a curva e o retângulo pra poder visualizar melhor o que a questão pede, então calculamos a maior área possível, quer dizer, precisaremos calcular um ponto de máximo.

Passo 2

Colocando no gráfico a curva e desenhando um retângulo, temos:

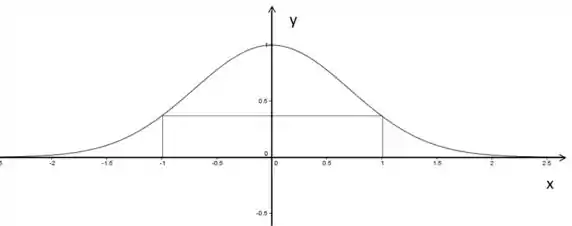
O retângulo tá com base no eixo x e o vértice no primeiro quadrante tá no ponto , então o comprimento dele é e a altura é certinho? No primeiro quadrante ;)

Passo 3

Agora a área desse retângulo será e como precisamos achar a maior área vamos derivar essa função área e igualar a zero, ok?

Como...

Derivando essa equação

Passo 4

Agora se você observar (substituindo em ), vai notar que

para

então é um máximo global e é a inflexão da nossa ! Como a curva é simétrica o outro ponto será .

É isso, provamos que a maior área desse retângulo é com os vértices nos pontos de inflexão

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a Definição 2.2 . 1 para encontrar f ' x e, então, encontre a reta tangente ao gráfico de y = f x em x = a . f x = 1 x 2 ; a = - 1

Use a Definição 2.2 . 1 para encontrar f ' x e, então, encontre a reta tangente ao gráfico de y = f x em x = a . f x = 2 x + 1 ; a = 4

Use a Fórmula 12 para encontrar d y d x . y = x 2 - x

Use a Fórmula 12 para encontrar d y d x . y = x 4

Use a Definição 2.2 . 1 (com a mudança apropriada na notação) para obter a derivada pedida.Encontre d V d r se V = 4 3 π r 3 .